Parámetros de la Onda Senoidal (CA): Frecuencia, Periodo y Valor Eficaz (RMS)
Cuando decimos que un enchufe tiene 230 Voltios, estamos simplificando la realidad. En la Corriente Alterna, el voltaje nunca está quieto: sube, baja, cruza por cero y cambia de polaridad constantemente dibujando una Onda Senoidal.
Para poder estudiar y medir esta 'montaña rusa' eléctrica, necesitamos parámetros específicos que definan su comportamiento en el tiempo (como la Frecuencia y el Periodo) y su magnitud real (como el Valor Pico y el Valor Eficaz o RMS).
En esta guía desglosamos las matemáticas que esconden nuestros aparatos eléctricos cuando son alimentados por corriente alterna.
El objetivo de esta guía es analizar los parámetros técnicos de la corriente alterna, tanto básicos como complejos. La combinación de teoría, práctica y fórmulas nos dará una comprensión completa de los conceptos que definen y caracterizan la electricidad de uso diario.
Contenidos
- El Origen Matemático: Del Círculo a la Onda
- Ciclo de la Corriente Alterna
- Frecuencia (f)
- Período (T = 1/f)
- Velocidad Angular (ω = 2πf)
- Valor Instantáneo (v(t))
- Valor Máximo o Valor Pico (Vmáx o Vp)
- Valor Pico a Pico (Vpp)
- Valor Medio o Promedio (Vmedio)
- Valor Eficaz o RMS (Vrms = Vmáx / √2)
- Ángulo de Fase: Ángulo Inicial de Una sola Onda
- Desfase (φ): Ángulo entre Dos Ondas
El Origen Matemático: Del Círculo a la Onda
Para analizar la corriente alterna, primero debemos entender su forma. Aunque en la electrónica moderna existen muchas formas de onda (cuadradas, triangulares, en diente de sierra, etc.), la CA generada y distribuida por las compañías eléctricas adopta una forma específica y fundamental: la onda sinusoidal (o senoidal).
Pero, ¿Por qué una onda sinusoidal? La respuesta se encuentra en la física de su generación. La electricidad en las centrales eléctricas (ya sean hidroeléctricas, térmicas o nucleares) no se crea de forma estática; se genera mediante el principio de inducción electromagnética, descrito por la Ley de Faraday.
Este principio establece que se induce un voltaje (y por tanto una corriente) en un conductor (una bobina de cable) cuando este se expone a un campo magnético variable. Este voltaje inducido es directamente proporcional a la rapidez con la que cambia en el tiempo el flujo magnético a través del conductor.
Movimiento Rotatorio del Generador de Corriente Alterna
El movimiento rotatorio es el corazón de la generación de corriente alterna senoidal. Para entenderlo a fondo, debemos analizar los 2 componentes principales de un generador industrial:
● El rotor: es un electroimán (campo magnético giratorio) alimentado por una fuente de corriente continua (llamada "excitación"). Esto permite controlar con precisión la intensidad del campo magnético. Su rotación es impulsada por una fuente de energía mecánica externa (turbina de vapor, agua, gas o un motor eólico).
● El estator: está compuesto por bobinas de cable, fijadas en la carcasa del generador para maximizar la captación del flujo magnético. Suelen tener núcleos de material ferromagnético (como hierro laminado) que concentran y guían las líneas de fuerza del campo magnético del rotor, aumentando así la eficiencia de la inducción.
El aspecto fundamental es la proyección del movimiento circular del rotor respecto al estator.

Indiferencia del Movimiento Relativo del Generador
El voltaje generado en los devanados (bobinas) por el fenómeno de la inducción electromagnética, se produce al existir un movimiento relativo entre el campo magnético y los conductores de las bobinas.
Es indiferente que se mueva el campo magnético respecto a las bobinas o viceversa, siempre que haya movimiento relativo entre ambos. Esto es una consecuencia directa del principio de relatividad en el electromagnetismo. No obstante, la configuración más común en grandes generadores es la que se ha indicado antes:
– Campo magnético móvil: es más eficiente y sencillo hacer girar el electroimán (de menor peso y complejidad para conducir altas corrientes) que hacer girar las pesadas bobinas del estator que generarán la alta corriente de salida.
– Conductores de las bobinas fijas: permite conectar los cables de salida de energía de forma directa y robusta, sin necesidad de complicados anillos de contacto giratorios para la potencia principal.
Proyección del Movimiento Circular
Para analizarlo de forma sencilla, podemos considerar el alternador elemental, que es el modelo teórico más simple. En este alternador, el campo magnético es fijo y creado por un imán permanente. El elemento móvil es una bobina de una sola espira.
Cada extremo de la espira está conectado a un anillo rozante. Unas escobillas de carbón frotan contra estos anillos, manteniendo el contacto eléctrico continuo mientras la espira gira.
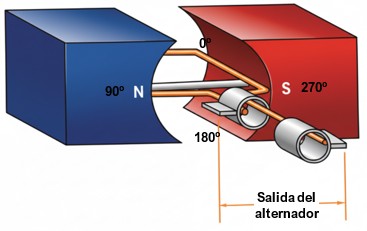
El movimiento de rotación uniforme se traduce matemáticamente en una señal sinusoidal:
- Ángulo de giro α = 0º: cuando la bobina se encuentran en 0 grados, los conductores se mueven paralelos al campo magnético. La tasa de cambio del flujo es momentáneamente cero, induciendo cero voltios.
- Ángulo de giro α = 90º: la bobina se enfrenta directamente al polo norte del imán. Los cables de la bobina se mueven perpendiculares al campo magnético induciendo el voltaje pico positivo.
- Ángulo de giro α = 180º: los cables de la bobina se vuelven a mover paralelos al campo magnético. La tasa de cambio del flujo vuelve a cero, induciendo cero voltios.
- Ángulo de giro α = 270º: la bobina se enfrenta al polo sur del imán. La tasa de cambio es nuevamente máxima, pero en la dirección opuesta. Esto induce el voltaje pico negativo.
- Ángulo de giro α = 360º: el ciclo se completa y se vuelve al punto de inicio.
Si graficamos el voltaje inducido (en el eje Y) contra el ángulo de rotación (en el eje X), la curva resultante es, por definición matemática, una función seno, en la que v(t) es proporcional al “sen α”. Por tanto, la onda sinusoidal no es una elección arbitraria; es la forma de onda más pura y natural que resulta de la conversión de energía mecánica rotatoria en energía eléctrica.
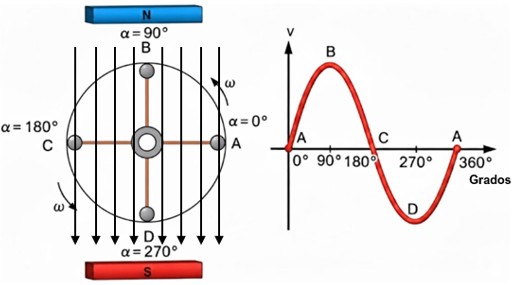
Ciclo de la Corriente Alterna
Para analizar los parámetros de la corriente alterna, utilizamos un gráfico de coordenadas. Este gráfico es la herramienta visual esencial para cualquier técnico.
– Eje vertical (eje Y): representa la amplitud o magnitud instantánea de la señal. Esta magnitud puede ser el voltaje (V) o la corriente (I).
– Eje horizontal (eje X): representa el progreso de la onda. Puede medirse en unidades de tiempo (t), generalmente en segundos o milisegundos, o en ángulo (α), medido en grados (0° a 360°) o radianes (0 a 2π).
Este gráfico nos permite "congelar" la onda en el tiempo y medir sus características principales.
Al observar el gráfico, vemos un patrón que se repite. Esta unidad fundamental de repetición se denomina ciclo (o ciclo completo).
Un ciclo es la porción más pequeña de la forma de onda que, si se repite, reproduce la onda completa indefinidamente.
Podemos definir un ciclo de varias maneras, pero la más común es:
- Comienza en el punto cero (0 V).
- Atraviesa el semiciclo positivo, donde todos los valores de voltaje son positivos, alcanzando un valor máximo (pico positivo).
- Regresa a cero, pero continúa en dirección negativa.
- Atraviesa el semiciclo negativo, donde todos los valores son negativos, alcanzando un valor máximo negativo (pico negativo).
- Regresa a cero, con la misma dirección y pendiente que tenía al inicio, listo para comenzar la siguiente repetición.
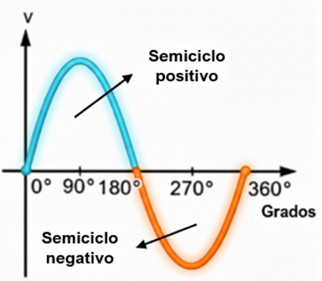
Este ciclo completo representa una rotación completa (360° o 2π radianes) del generador que la creó (considerando el generador elemental de 1 par de polos). La comprensión del ciclo es la base para definir los parámetros temporales más importantes de la corriente alterna: la frecuencia y el período.
Frecuencia (f)
La frecuencia es, sin duda, uno de los parámetros más importantes y definitorios de la corriente alterna. Si imaginamos la onda sinusoidal como una cuerda que sube y baja, la frecuencia nos dice qué tan rápido se produce esa oscilación. Es el "ritmo" o el "pulso" del sistema eléctrico.
Definición de la Frecuencia
Técnicamente, la frecuencia (f) se define como el número de ciclos completos que una forma de onda de corriente alterna (CA) realiza en el lapso de un segundo.
Como vimos en el punto anterior, un ciclo es la repetición completa de la onda (una rotación de 360° del generador elemental de un par de polos). Por lo tanto, si una onda completa un ciclo 50 veces exactas en un segundo, su frecuencia es de 50 ciclos por segundo. Si lo hace 60 veces, es de 60 ciclos por segundo.
Esta medida es fundamental porque establece el marco temporal para todos los demás fenómenos reactivos (inductivos y capacitivos) en un circuito de CA.
En el Sistema Internacional de Unidades (SI), la frecuencia se mide en Hercios (o Hertz), en honor al físico alemán Heinrich Hertz, quien fue el primero en demostrar experimentalmente la existencia de las ondas electromagnéticas.
El símbolo es Hz.
Un Hercio (1 Hz) es la frecuencia de un evento periódico que completa un ciclo por segundo.
Por lo tanto, las definiciones de nuestros ejemplos se expresan de la siguiente manera:
– 50 ciclos/segundo = 50 Hz
– 60 ciclos/segundo = 60 Hz
Frecuencia 50 Hz contra 60 Hz
A diferencia de otros parámetros de la corriente alterna como el voltaje, que pueden variar, la frecuencia de la red eléctrica es un valor extremadamente estable y estandarizado a nivel nacional. Globalmente, el mundo se divide principalmente en 2 "zonas de frecuencia":
● Red eléctrica a 50 Hz: es el estándar utilizado en la gran mayoría del mundo, incluyendo toda Europa, gran parte de Asia, África, Australia y partes de Sudamérica.
● Red eléctrica a 60 Hz: es el estándar dominante en América del Norte (Estados Unidos, Canadá o México), la mayor parte de Sudamérica (incluyendo Brasil, Colombia o Venezuela) y algunos países de Asia (como Corea del Sur, Filipinas o Taiwán).
Esta división es un legado histórico de finales del siglo XIX, basado en las decisiones de ingeniería de las primeras compañías eléctricas (como AEG en Alemania para 50 Hz y Westinghouse en EE.UU. para 60 Hz).

Hoy en día, esta diferencia es una de las principales barreras para la interconexión de redes eléctricas continentales y la razón por la que muchos aparatos eléctricos no son universalmente compatibles.
Importancia de la Frecuencia
La frecuencia no es solo un número; es una variable de diseño fundamental que tiene un impacto directo y profundo en el comportamiento y la construcción de los equipos eléctricos.
Velocidad de Motores de Inducción
La velocidad de rotación de los motores de CA más comunes (los motores de inducción asíncronos) está directamente determinada por la frecuencia de la red y el número de polos magnéticos del motor. La velocidad síncrona (la velocidad del campo magnético giratorio) se calcula con:

donde:
n = velocidad síncrona en r.p.m. (revoluciones por minuto)
f = frecuencia de la red (Hz)
p = pares de polos del motor
Ejemplo: Un motor de 4 polos (2 pares, p = 2) conectado a 50 Hz tendrá una velocidad síncrona de (60 · 50) / 2 = 1.500 rpm. El mismo motor conectado a 60 Hz girará un 20% más rápido, a (60 · 60) / 2 = 1.800 rpm. Usar un motor diseñado para 50 Hz en una red de 60 Hz lo acelerará, aumentando el desgaste y la potencia consumida, y potencialmente quemándolo.
Diseño de Transformadores
El funcionamiento de un transformador se basa en un flujo magnético variable en su núcleo. El tamaño del núcleo de hierro necesario es inversamente proporcional a la frecuencia.
– A 60 Hz (mayor frecuencia): se necesita un núcleo más pequeño para manejar la misma potencia.
– A 50 Hz (menor frecuencia): se necesita un núcleo magnético más grande y robusto.
⚠️Peligro: Si se conecta un transformador diseñado para 60 Hz a una red de 50 Hz, el núcleo (que es demasiado pequeño para esa baja frecuencia) se saturará magnéticamente. Esto provoca que la bobina primaria pierda su impedancia, generando un pico masivo de corriente (casi un cortocircuito) que lo destruirá por sobrecalentamiento.
Reactancia
Este es el concepto más importante. La frecuencia es un componente directo en el cálculo de la oposición a la corriente alterna en bobinas (inductores) y condensadores (capacitores).
● Reactancia inductiva (XL): XL = 2π f L. Aumenta con la frecuencia.
● Reactancia capacitiva (XC): XC = 1 / (2 π f C). Disminuye con la frecuencia.
Esto significa que todos los circuitos que dependen de estos componentes (filtros en fuentes de alimentación, sistemas de corrección de factor de potencia, balastos de iluminación fluorescente) están diseñados para operar a una única y específica frecuencia.
Período (T = 1/f)
Si la frecuencia (f) nos dice cuántos ciclos ocurren en un segundo, el período (T) responde a la pregunta complementaria: ¿cuánto tiempo dura un solo ciclo?
Es uno de los parámetros fundamentales para el análisis temporal de la corriente alterna, especialmente cuando se trabaja con osciloscopios o se diseñan circuitos de control y temporización, donde la duración en milisegundos de cada ciclo es la variable de diseño principal.
Definición del Período
El período (T) es la cantidad de tiempo, medido en segundos (s), que una forma de onda de corriente alterna tarda en completar un ciclo completo.
Es la duración de la unidad fundamental de repetición. Si medimos el tiempo desde que la onda cruza el cero en sentido positivo hasta la próxima vez que cruza el cero en el mismo sentido, ese lapso de tiempo es el Período.
La relación entre el período y la frecuencia es una de las más importantes y directas en toda la física de ondas: son inversamente proporcionales.
– Si la frecuencia es alta (muchos ciclos por segundo), el tiempo disponible para cada ciclo debe ser muy corto.
– Si la frecuencia es baja (pocos ciclos por segundo), el tiempo para cada ciclo será, en consecuencia, largo.
Matemáticamente, el período es el recíproco (o inverso) de la frecuencia. La relación se expresa con una fórmula simple y fundamental:
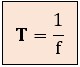
donde:
T = período, medido en segundos (s).
f = frecuencia, medida en Hercios (Hz).
De igual manera, si se conoce el período (por ejemplo, midiéndolo en un osciloscopio), se puede calcular la frecuencia:
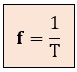
Ejemplos de Cálculo del Período
Apliquemos la fórmula a los 2 estándares de red eléctrica mundiales:
● Red de 50 Hz (Europa, Asia, etc.): la frecuencia es de 50 Hz (es decir, 50 ciclos por segundo). El cálculo del Período es: T = 1 / 50 Hz = 0,02 s.
Valor práctico: en el trabajo técnico diario, 0,02 segundos es un valor pequeño, por lo que comúnmente se expresa en milisegundos (ms): 0,02 · 1000 ms/s = 20 ms.
Por tanto, un ciclo completo de la red europea dura 20 milisegundos. Esto implica que el semiciclo positivo dura 10 ms y el semiciclo negativo dura otros 10 ms.

● Red de 60 Hz (América, etc.): la frecuencia es de 60 Hz (es decir, 60 ciclos por segundo). El cálculo del Período es: T = 1 / 60 Hz = 0,01667 s.
Valor práctico: convirtiendo a milisegundos (ms): 0,01667 · 1000 ms/s = 16,67 ms.
Por tanto, la onda de la red americana de 60 Hz es "más rápida", completando su ciclo en solo 16,67 milisegundos.

Importancia del Período
El período no es solo un dato derivado; es el parámetro principal en ciertas áreas:
● Medición con osciloscopio: en un laboratorio, a menudo es más fácil y preciso medir el período visualmente.
Se ajusta la base de tiempo (la escala "tiempo/división" del eje horizontal) y se mide cuántas divisiones ocupa un ciclo. Si un ciclo ocupa 4 divisiones y la base de tiempo es 5 ms/div, el período es 4 · 5 = 20 ms. A partir de ahí, se calcula la frecuencia: f = 1 / 0,020 = 50 Hz.
● Electrónica de potencia: en el diseño de dimmers (reguladores de luz) o variadores de velocidad, que a menudo usan componentes como TRIACs o SCRs, el control se ejerce dentro de un solo ciclo.
Estos dispositivos se "disparan" en un momento específico, por ejemplo, "a los 5 milisegundos de haber iniciado el ciclo". Por lo tanto, el diseño de estos circuitos de control se basa fundamentalmente en el período (20 ms o 16.67 ms) como la ventana de tiempo operativa.
Velocidad Angular (ω = 2πf)
Si bien la frecuencia (f) y el período (T) nos dan una medida práctica y "externa" de la onda (cuántos ciclos por segundo o cuántos segundos por ciclo), la velocidad angular, representada por la letra griega omega minúscula ω, es uno de los parámetros matemáticos fundamentales de la corriente alterna.
Al igual que en un coche la velocidad lineal es la distancia recorrida dividida por el tiempo, en un sistema rotatorio (como el generador eléctrico): la Velocidad Angular ω es el Ángulo (α) recorrido dividido por el Tiempo (t) que ha tardado en recorrerlo.
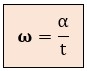
donde:
ω = velocidad angular, en radianes por segundo (rad/s)
α = ángulo, en radianes (rad)
t = tiempo, en segundos (s)
La velocidad angular recibe el nombre de frecuencia angular en física y matemáticas, describiendo la frecuencia, en radianes por segundo, de cualquier movimiento oscilatorio (no solo eléctrico, como un péndulo o un muelle).
También recibe el nombre de pulsación de la corriente, siendo este término más "propio" del campo de la electricidad y las telecomunicaciones. Se refiere a la rapidez de la oscilación o "pulso" de la onda. Cuando se habla de la ω de la red eléctrica, es muy común que los técnicos se refieran a ella simplemente como "la pulsación".
Definición de la Velocidad Angular
La velocidad angular (ω) describe la velocidad de la onda en términos de radianes por segundo (rad/s). En lugar de contar "ciclos" completos, mide la tasa de cambio del ángulo de fase de la onda por unidad de tiempo.
Recordemos que la onda sinusoidal de CA es la proyección de un movimiento circular debido al giro del generador:
– Frecuencia (f): mide la velocidad en "ciclos por segundo". Es una medida de conteo.
– Velocidad angular (ω): mide la velocidad en "radianes por segundo". Es una medida de rotación.
Para conectar ambos conceptos, necesitamos una equivalencia entre "ciclos" y "radianes". En matemáticas y física, un círculo completo (es decir, un ciclo) no se mide en 360°, sino en 2π radianes.
1 ciclo = 360º = 2π radianes
Con esta equivalencia, la conversión es directa:
Si la frecuencia (f) es el número de ciclos en un segundo, y cada ciclo son 2π radianes, entonces la velocidad angular (ω) es simplemente la frecuencia multiplicada por 2π.
Esta relación nos da una de las fórmulas más utilizadas en el análisis de CA. La pulsación de la corriente ω es:
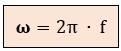
donde:
ω = velocidad angular, en radianes por segundo (rad/s)
f = frecuencia, en Hercios (Hz)
Ejemplo: Calculemos el valor de ω para las 2 frecuencias de red estándar. Estos valores son tan comunes que los ingenieros a menudo los memorizan:
– Red de 50 Hz (Europa, etc.):
ω = 2π · 50 = 100 π ≈ 314,16 rad/s
– Red de 60 Hz (América, etc.):
ω = 2π · 60 = 120 π ≈ 376,99 rad/s (a menudo redondeado a 377 rad/s en libros de texto)
Relación entre la Velocidad Angular y la Velocidad de Rotación
– Velocidad angular eléctrica (ω): parámetro matemático de la corriente alterna que describe la rapidez con la que la onda sinusoidal progresa. Es la velocidad del "fasor" que representa la onda. Se mide en rad/s.
– Velocidad angular mecánica (n): velocidad física a la que gira el eje del alternador (el rotor) en la central eléctrica. Se suele medir en revoluciones/minuto (revoluciones por minuto o rpm).
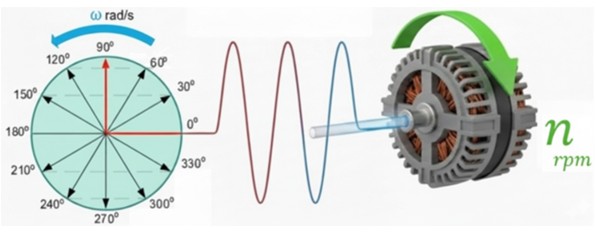
Pero, ¿cómo se relacionan estas 2 velocidades?
Imaginemos el generador más simple posible: un alternador de 1 par de polos. Para generar la onda sinusoidal el rotor debe dar una revolución completa (360° físicos). En el caso de 1 par de polos, hay una correspondencia directa 1:1. Por tanto, 1 revolución mecánica = 1 ciclo eléctrico.
Dado que la revolución y el ciclo ocurren en el mismo lapso de tiempo (el período, T), sus velocidades angulares deben ser idénticas, ω = n (ambas en rad/s). Comparamos ω y n en la misma unidad:
1º) Convertimos n de rpm a rad/s:
- Dividimos por 60 para pasar a revoluciones/segundo = n/60
- Multiplicamos por 2π para pasar a radianes/segundo = (n/60) · 2π
2º) Como ω = n (ambas en rad/s):
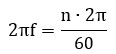
3º) Simplificamos la ecuación:
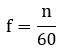
4º) La velocidad n, en r.p.m. es:
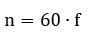
Esta simple fórmula revela la velocidad n a la que debe girar un generador de 2 polos (1 par de polos) para producir nuestras frecuencias de red:
● Para generar 50 Hz (Europa): n = 60 · 50 = 3.000 rpm
● Para generar 60 Hz (América): n = 60 · 60 = 3.600 rpm

Si una máquina tiene más polos, como 4 polos (2 pares de polos), generará 2 ciclos eléctricos por cada revolución mecánica. En ese caso, la velocidad mecánica sería la mitad: 1500 rpm para 50 Hz, según la fórmula general:

Importancia de la Velocidad Angular
Podría parecer un parámetro de la corriente alterna puramente académico, pero la velocidad angular ω es la piedra angular de las 2 fórmulas más importantes en el cálculo de CA:
● Fórmula general de la onda (valor instantáneo): como veremos en detalle más adelante, la "receta" para describir el voltaje en cualquier instante de tiempo t es:
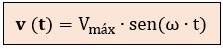
Analicemos el término ω · t:
ω = en radianes / segundo
t = en segundos
Por lo tanto, ω · t nos da el ángulo instantáneo α en radianes.
Esta multiplicación convierte el tiempo transcurrido (t) en una posición angular α (en radianes) dentro del ciclo, permitiendo que la función seno calcule el voltaje correspondiente en ese preciso instante. Sin la velocidad angular ω, la fórmula no funcionaría.
● Cálculo de reactancia (oposición a la CA): la velocidad angular es el componente principal para definir la reactancia, que es la oposición al flujo de la CA por parte de bobinas (inductores) y condensadores (capacitores).
– Reactancia inductiva (XL): es la oposición de una bobina. Es directamente proporcional a la velocidad de la onda:
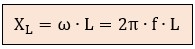
– Reactancia capacitiva (XC): es la oposición de un condensador. Es inversamente proporcional a la velocidad de la onda:
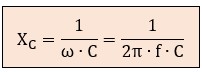
Como se puede ver, usar ω en lugar de 2π · f no solo simplifica las ecuaciones, sino que también refuerza el concepto de que la oposición de estos componentes está fundamentalmente ligada a la "velocidad de rotación" del sistema eléctrico.
Valor Instantáneo (v(t))
El valor instantáneo es la magnitud exacta, ya sea de voltaje o de corriente, en un instante de tiempo específico (t).
A diferencia de la corriente continua (CC), donde un voltaje puede definirse con un solo número (p.ej., V = 12 V), en la corriente alterna (CA) el valor está en perpetuo cambio. Por lo tanto, una simple medida de "voltaje" no es suficiente; necesitamos saber el voltaje en un momento preciso.
El valor instantáneo se denota como una función matemática:
– v(t) para el voltaje instantáneo.
– i(t) para la corriente instantánea.
Esta notación v(t) significa "el valor del voltaje (v) en función del tiempo (t)". Es la descripción más completa y fundamental de la onda de CA. Si pudiéramos "pausar" el tiempo y medir la tensión con un voltímetro ideal en un instante t, el valor que leeríamos sería v(t).
Para cualquier onda sinusoidal pura, existe una fórmula general que nos permite calcular el valor instantáneo en cualquier momento t, siempre que conozcamos las 3 características definitorias de la onda.
La fórmula general para el voltaje instantáneo es:
● v(t) = Vmáx · sen (ω· t + φ)
De manera análoga, para la corriente instantánea, la fórmula es:
● i(t) = Imáx · sen (ω· t + φ)
Si el ángulo φ, o desfase inicial, en el que las ondas se encontraban en el momento t = 0 es φ = 0, el valor instantáneo de la tensión y la corriente serían respectivamente de:
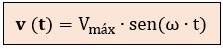

A continuación, analizaremos la fórmula del voltaje, pieza por pieza:

Voltaje Instantáneo v(t)
Es el resultado de la ecuación. Es el valor del voltaje (en Voltios) en el preciso instante de tiempo t que nos interesa.
Ejemplo: Si calculamos v(0,005 s) y el resultado es 325 V, significa que a los 5 milisegundos de iniciado el ciclo, el voltaje alcanzó los 325 Voltios.
Valor máximo, Valor Pico o Amplitud (Vmáx)
Es el valor máximo (la "cresta") que la onda alcanza en su ciclo. Define la "altura" total de la onda.
Actúa como el multiplicador o escalador. La función seno por sí sola solo produce valores entre -1 y +1. El valor de pico Vmáx "estira" esta onda de ±1 a la magnitud real del voltaje (p.ej., ±325 V). Se mide en Voltios (V).
La Función Seno (sen)
Es el "corazón" de la fórmula. Se trata de la función trigonométrica que genera la forma de onda sinusoidal característica (la subida suave, el pico, la bajada, el valle y la vuelta al inicio).
Es el generador de la forma de onda. Toma un ángulo como entrada y devuelve un valor entre -1 y +1.
El Argumento o Ángulo Total (ω · t + φ)
Es la expresión completa dentro del paréntesis de la función seno. Se trata del ángulo total de la onda en el instante t.
Es muy importante entender que este ángulo se mide en Radianes (rad). Para que la fórmula funcione, ω debe estar en rad/s y t en segundos.
⚠️¡Advertencia de Cálculo!
Al usar esta fórmula en una calculadora científica, debemos asegurarnos de que la calculadora esté en modo RAD (Radianes), no en modo DEG (Degrees o grados). Este es el error más común en los cálculos de CA.
Ángulo de Progreso (ω · t)
Este término es el producto de la Velocidad Angular (ω) (en rad/s) y el Tiempo (t) (en s).
Como vimos antes, ω = 2 π · f, es la velocidad a la que "gira" la onda (p.ej., 314,16 rad/s para 50 Hz).
Al multiplicar ω · t, estamos calculando qué ángulo ha recorrido la onda desde el inicio (t = 0) hasta el instante t (suponiendo que en ese instante φ = 0).
Ejemplo: A 50 Hz (ω ≈ 314,16 rad/s), en t = 0,005 s, el ángulo recorrido es 314,16 · 0,005 = 1,5708 radianes (que es exactamente π/2, o 90°).
Ángulo de Fase o Desfase Inicial (φ)
Es el "punto de partida" de la onda. Representa el ángulo en el que la onda ya se encontraba en el momento t = 0. Es un desplazamiento horizontal (un offset):
– Si φ = 0: la onda v(t) = Vmáx · sen (ω · t) es una onda seno pura: comienza en 0 V, sube hacia positivo y sigue su ciclo.
– Si φ ≠ 0: la onda está "adelantada" o "atrasada" en el tiempo. Por ejemplo, una onda coseno es simplemente una onda seno con un desfase de +π/2 radianes (o +90°).
Este parámetro es vital para comparar 2 ondas, como la de voltaje y la de corriente, para determinar el factor de potencia. Se mide en radianes (rad).
Más adelante se hablará del desfase φ entre las ondas de tensión y corriente, que será la diferencia angular entre ellas. No obstante, para simplificar el análisis, casi siempre tomamos una de las ondas como nuestra "referencia" (φ = 0, para t = 0). En los sistemas de potencia, la onda de voltaje v(t) se usa casi universalmente como la referencia.
Valor Máximo o Valor Pico (Vmáx o Vp)
Mientras que el valor instantáneo nos da el voltaje en un momento cualquiera, el valor máximo o valor pico es el valor específico más importante de la amplitud: es la magnitud máxima que la onda alcanza en cualquier punto de su ciclo.
El valor pico (Vmáx o Vp), también conocido como amplitud, es el valor instantáneo máximo que adquiere una onda de corriente alterna. Es la "altura" máxima de la onda medida desde el punto de referencia central (cero) hasta el punto más alto de su cresta.
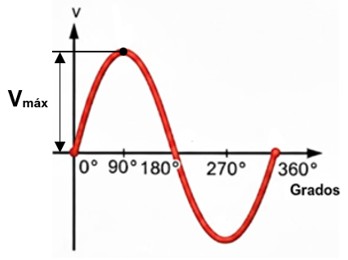
En una onda sinusoidal simétrica, que es el estándar en las redes de potencia, existen 2 picos por cada ciclo:
– Pico positivo (+Vmáx): el valor máximo alcanzado durante el semiciclo positivo.
– Pico negativo o valle (-Vmáx): el valor máximo alcanzado en la dirección opuesta durante el semiciclo negativo.
Técnicamente, el valor máximo o "valor pico" se refiere a la magnitud (el valor absoluto) de esta cresta. Por ejemplo, si el pico positivo es +325 V, el pico negativo será -325 V, y el valor máximo (Vmáx) o valor pico (Vp) es 325 V.
Rol del Valor Máximo en la Fórmula General de la Onda
Como ya se introdujo antes, el valor máximo o pico es el multiplicador de amplitud en la ecuación fundamental de la onda:

La función sen (ω · t + φ) por sí sola solo puede generar valores que oscilan entre +1 y -1. Es el Vmáx el que escala esta forma de onda normalizada a las dimensiones eléctricas reales del circuito.
Cuando la función seno alcanza su valor máximo (+1), el voltaje instantáneo es:
v(t) = Vmáx · (1) = Vmáx
Y cuando alcanza su valor mínimo (-1):
v(t) = Vmáx · (-1) = -Vmáx
Importancia Técnica del Valor Máximo
Aunque el valor máximo no es el que usamos para calcular la potencia (para eso usaremos el valor eficaz o RMS), constituye uno de los parámetros de la corriente alterna de especial importancia por 2 razones principales:
● Tensión de aislamiento: los componentes eléctricos, especialmente los aislamientos de los cables, los condensadores y los semiconductores (como diodos y transistores), deben ser capaces de soportar el Valor Pico de la tensión sin fallar (sin que se produzca una ruptura dieléctrica).
● Referencia de cálculo: es el valor base desde el cual se calculan matemáticamente todos los demás valores de amplitud (RMS, promedio o pico a pico).
Ejemplo: Un error común de principiante es pensar que un cable para una red de 230 V solo necesita soportar 230 V. Esto es incorrecto. Los 230 V son el valor eficaz o RMS (que veremos más adelante). El valor máximo o valor pico en esa red es:
Vmáx = Vrms · √2 ≈ 230 V · 1,414 = 325,2 V
Por lo tanto, el aislamiento del cable debe estar diseñado para soportar picos de al menos 325 V (y en la práctica, mucho más, por seguridad) que ocurren 100 veces por segundo (en una red de 50 Hz).
Valor Pico a Pico (Vpp)
Mientras que el valor máximo o valor pico (Vp) describe la amplitud máxima desde el centro (cero), el valor pico a pico (Vpp) describe la "altura" total de la onda, desde su punto más bajo hasta su punto más alto.
El valor pico a picoes la medida de la excursión total de la forma de onda. Representa el voltaje (o corriente) total medido desde el pico negativo (valle) hasta el pico positivo (cresta).
Es, literalmente, la diferencia de potencial entre el valor instantáneo máximo (+Vmáx) y el valor instantáneo mínimo (-Vmáx) del ciclo.
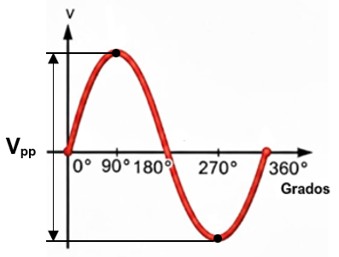
Fórmula del Valor Pico a Pico
Para una onda sinusoidal simétrica estándar (que oscila alrededor de 0 V), el cálculo es simple. Es la suma de la magnitud del pico positivo y la magnitud del pico negativo.
Para la onda eléctrica del voltaje será:
Vpp = (+Vmáx) - (-Vmáx) = Vmáx + Vmáx = 2 · Vmáx
De manera similar, para la corriente:
Ipp = (+Imáx) - (-Imáx) = Imáx + Imáx = 2 · Imáx
Uso y Aplicación del Valor Pico a Pico
Se podría pensar que Vpp es un valor redundante si ya conocemos Vmáx o Vp, pero es el parámetro preferido en campos específicos, principalmente la electrónica de señales y en el uso de osciloscopios.
La razón principal es que el Vpp es independiente del punto de referencia de "cero voltios".
● Mediciones en osciloscopios: el osciloscopio es la herramienta fundamental para visualizar señales eléctricas. Medir el Vpp en su pantalla es la tarea más directa:
El técnico simplemente mide la altura total de la onda usando la cuadrícula (divisiones verticales) y la multiplica por la escala (Voltios/División).
● Electrónica de señales (audio, RF, comunicaciones): las señales de CA (como una señal de audio) a menudo no oscilan alrededor de 0 V. Es muy común que una pequeña señal de CA esté "montada" sobre un nivel de corriente continua (CC) más grande. Esto se llama componente de CC o DC offset.
Ejemplo: Imaginemos una señal de audio de 1 V de amplitud (CA) que "flota" sobre un nivel de polarización de 5 V (CC).

La onda no oscilará entre +1 V y -1 V. Oscilará entre un máximo de 5 V + 1 V = 6 V (pico positivo) y un mínimo de 5 V - 1 V = 4 V (pico negativo).
Si intentamos medir el Vmáx o Vp de esta señal, el resultado es confuso. ¿Es 6 V (el pico real) o 1 V (la amplitud de la CA)? El valor pico a pico Vpp es inequívoco.
Vpp = pico máximo - pico mínimo = 6 V – 4 V = 2 V
Por esta razón, Vpp es el parámetro estándar para describir el rango dinámico y la magnitud de las señales en el diseño de amplificadores, filtros y sistemas de comunicación.
Valor Medio o Promedio (Vmedio)
El valor medio (o valor promedio) es un concepto que a menudo genera confusión debido a una peculiaridad matemática de la onda sinusoidal. Para entenderlo, debemos distinguir entre la definición matemática estricta y la definición práctica utilizada en ingeniería.
¿Por qué el promedio es cero? Si aplicamos la definición matemática estándar de "promedio" (la suma de todos los valores dividida por la cantidad de valores) a un ciclo completo de una onda sinusoidal pura, nos encontramos con un resultado contraintuitivo.
– Durante el semiciclo positivo: el voltaje sube y baja, acumulando un "área" positiva bajo la curva.
– Durante el semiciclo negativo: el voltaje hace exactamente lo mismo, pero con polaridad invertida, acumulando un "área" negativa idéntica.
Al sumar el área positiva y la negativa a lo largo de un ciclo completo (360º o 2π), estas se cancelan mutuamente de forma perfecta.
Vpromedio del ciclo completo = 0 V
Matemáticamente es correcto, pero eléctricamente es un dato inútil. Decir que el voltaje promedio de un enchufe es "0 voltios" no nos ayuda a diseñar circuitos ni describe la energía real que transporta la onda.
Valor Medio de Medio Ciclo
Para que este parámetro tenga utilidad práctica en electricidad, se redefinió el concepto. Cuando hablamos del “valor medio” o "valor promedio" en corriente alterna, nos referimos implícitamente al promedio de un solo semiciclo (o lo que es lo mismo, al promedio del valor absoluto de la onda senoidal, conocido como onda rectificada).
Imaginemos que tomamos solo el semiciclo positivo de la onda (de 0 a π radianes) y calculamos su altura media geométrica. Este valor representa el equivalente en corriente continua si "aplanáramos" esa semionda para rellenar los valles, manteniendo la misma área total.
El cálculo se realiza integrando la función seno sobre medio ciclo y dividiendo por la longitud de la base (π). El resultado es una constante fundamental:
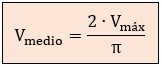
2 ⋅ Vmáx = área de medio ciclo (integral de 0 a π de la función Vmáx · sen (ω · t) → Vmáx · sen (α)
π = longitud de la base. El promedio de cualquier conjunto de datos es la suma total (el área), dividida entre el número de elementos (la longitud de la base).
La expresión 2/π es una constante, cuyo valor es ≈ 0,637.
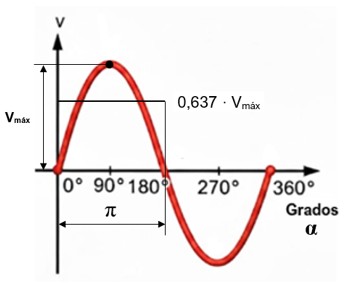
Por tanto, el valor medio o valor promedio de una corriente alterna sinusoidal es aproximadamente el 63,7% de su valor pico, que valdría tanto para el voltaje como para la corriente:
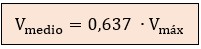
Aplicaciones Prácticas del Valor Medio
Aunque el valor eficaz o RMS (que veremos a continuación) es el rey para los cálculos de potencia y calentamiento, el valor medio tiene su propio nicho de importancia.
● Rectificación y fuentes de alimentación: cuando rectificamos la CA, es decir convertimos CA en CC usando diodos, lo que obtenemos inicialmente es una onda pulsante compuesta solo por los semiciclos positivos. El voltaje de salida de CC "bruto" de un rectificador de onda completa, antes de ser filtrado por condensadores, es exactamente el valor medio.
● Transferencia de carga (galvanoplastia y baterías): el valor RMS calcula el calor, pero el valor medio calcula la transferencia de electrones. En aplicaciones electroquímicas, como cargar una batería o en procesos de galvanoplastia (recubrimiento de metales), la cantidad de material depositado o de carga almacenada depende del flujo neto de corriente, que está mejor representado por el valor medio (considerando la corriente rectificada que entra a la batería).
● Instrumentación antigua y económica: muchos multímetros analógicos antiguos (de aguja) y algunos digitales muy económicos funcionan internamente midiendo el valor medio de la señal, pero su escala está calibrada para mostrar el valor eficaz o RMS. Esto funciona bien para ondas sinusoidales puras, pero da errores enormes si se intenta medir ondas o distorsionadas, ya que la relación fija de 0,637 contra 0,707 deja de ser válida.
Valor Eficaz o RMS (Vrms = Vmáx / √2)
El valor eficaz, universalmente conocido como RMS, es la columna vertebral de la ingeniería eléctrica práctica. Es el lenguaje común en el que hablan los ingenieros, los electricistas, los fabricantes de equipos y las compañías eléctricas.
Como hemos visto, el voltaje de CA cambia constantemente de valor (de 0 V a un pico, vuelve a 0 V, baja a un pico negativo...). Si quisiéramos calcular la potencia de esta onda, ¿qué valor de voltaje usamos en la Ley de Ohm (P = V · I)?
– ¿El valor pico? No, porque la onda solo está en el pico un instante minúsculo.
– ¿El valor cero? No, porque eso implicaría que no hay energía.
– ¿El promedio? Como vimos, el promedio matemático es cero.
Necesitamos un valor que represente la "capacidad real de trabajo" de esa onda fluctuante. Ese valor es el RMS.
Nota: Cuando tomamos un multímetro y medimos el voltaje de un enchufe, el número que aparece en la pantalla (230 V, 120 V, etc.) es el valor RMS. A menos que se especifique explícitamente lo contrario, cualquier voltaje de CA mencionado en una ficha técnica o placa de características es siempre RMS.
Definición del Valor Eficaz o RMS
La definición de RMS no es intuitiva a simple vista, por lo que se explica mejor mediante una equivalencia energética con la corriente continua (CC).
El valor RMS de una corriente alterna es el valor equivalente de voltaje o corriente continua (CC) que produciría la misma cantidad de calor (disipación de potencia) en una resistencia idéntica.
Imaginemos 2 circuitos idénticos con una resistencia calefactora (como una estufa eléctrica):
– Circuito A: alimentado por una batería de 10 V CC.
– Circuito B: alimentado por un generador de CA.
Para que el circuito B caliente la resistencia exactamente a la misma temperatura y con la misma rapidez que el circuito A, el voltaje de CA debe tener un valor eficaz (RMS) de 10 V.
Curiosamente, para lograr este "efecto de 10 V", el generador de CA tendrá que alcanzar picos mucho más altos (de aprox. 14,14 V), pero su "eficacia" energética neta será igual a la de la batería de 10 V.
¿Qué Significa RMS?
RMS son las siglas en inglés de Root Mean Square (Raíz Cuadrática Media). Este nombre describe literalmente el proceso matemático estadístico para calcularlo a partir de cualquier forma de onda:
● Square (cuadrática): se elevan al cuadrado todos los valores instantáneos de la onda. Esto convierte todos los valores negativos del semiciclo negativo en positivos, ya que la potencia siempre es positiva: (-2)2 = 4.
● Mean (media): se calcula el promedio de esos valores al cuadrado.
● Root (raíz): se calcula la raíz cuadrada de ese promedio para volver a la escala original.
Valor Eficaz o RMS de la Onda Senoidal
Para una onda sinusoidal pura (y solo para esta forma de onda), la relación entre el valor máximo o valor pico (Vmáx) y el valor eficaz Vrms, o simplemente “V”, es una constante fija derivada de raíz de 2 (√2).
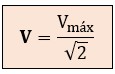
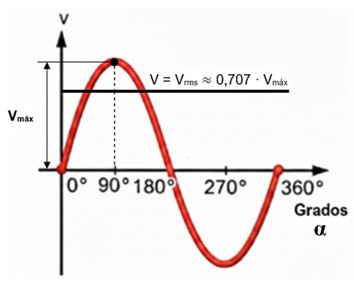
Dado que 1 / (√2) ≈ 0,707106, la fórmula práctica que todo electricista memoriza es:
Vrms ≈ 0,707 · Vmáx
Y de igual manera para la corriente:
Irms ≈ 0,707 · Imáx
La interpretación es que el valor eficaz es aproximadamente el 70,7% del valor máximo o pico de la onda.

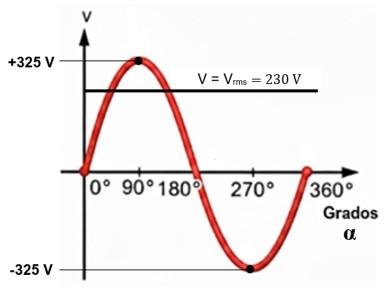
La Verdad sobre los 230 V
Este es el ejemplo que contextualiza todo. En Europa y gran parte del mundo, decimos que la tensión doméstica es de 230 V. En Estados Unidos, se habla de 120 V. Esta cifra es el Valor RMS.
Sin embargo, el aislamiento de los cables y los componentes electrónicos dentro de un cargador de móvil deben soportar la tensión real máxima que ocurre en cada ciclo (el valor máximo o valor pico). Si aplicamos la fórmula inversa, descubrimos la realidad oculta de nuestros enchufes.
Para diseñar circuitos o entender el estrés del aislamiento, a menudo necesitamos hallar el máximo partiendo del valor conocido RMS. Despejando la fórmula anterior:
Vmáx = √2 · Vrms ≈ 1,4142 · Vrms
Si tenemos una toma de corriente de 230 V (RMS), ¿cuál es el voltaje máximo que "golpea" nuestros aparatos 100 veces por segundo (en los picos positivos y negativos)?
Vmáx = 1,4142 · Vrms = 1,4142 · 230 ≈ 325 V
En conclusión, aunque lo llamamos "230 V", la onda oscila realmente entre +325 V y -325 V.
Por ejemplo, un condensador diseñado solo para 250 V explotaría instantáneamente si se conecta a la red de 230 V, porque no soportaría los picos de 325 V. Esta distinción entre RMS y máximo es vital para la seguridad y el diseño de componentes.
Ángulo de Fase: Ángulo Inicial de Una sola Onda
Hasta ahora hemos analizado la onda según su "altura" (amplitud) y su "anchura" o velocidad (frecuencia). Ahora, debemos analizar su posición horizontal. Aquí es donde entra el concepto de fase.
El ángulo de fase (representado por la letra griega φ) es el parámetro que nos indica el estado exacto de la onda en el preciso momento en que empezamos a medir el tiempo. Es el desplazamiento angular de la forma de onda respecto al punto de referencia estándar (generalmente el origen de coordenadas t = 0).
En una onda sinusoidal "perfecta" o estándar Vmáx · sen (ω · t), asumimos que en el instante t = 0, el voltaje es 0 y está subiendo hacia el positivo. Pero en el mundo real, cuando conectamos un osciloscopio o analizamos un circuito, el "tiempo cero" es arbitrario. Puede que empecemos a mirar la onda cuando el voltaje ya está en su pico máximo, o cuando está cruzando por cero hacia abajo.
El ángulo de fase φ es el valor matemático que "corrige" la fórmula para reflejar esta posición inicial.
El Desplazamiento Horizontal
El ángulo de fase desplaza la onda hacia la izquierda o hacia la derecha a lo largo del eje horizontal (eje del tiempo).
– Si φ = 0: la onda comienza en 0 V y sube.
– Si φ ≠ 0: la onda está desplazada. El punto de cruce por cero no coincide con el eje vertical.
La mejor forma de entender φ es observando la ecuación general en el instante inicial:

Si sustituimos t = 0 (el inicio): v (0) = Vmáx · sen (ω · 0 + φ) = Vmáx · sen (φ). Esta ecuación nos dice que: El valor del voltaje en el inicio (t = 0) depende exclusivamente del ángulo de fase.
Ejemplos de Ángulos de Fase
Veamos 3 ejemplos clásicos de valores de φ para visualizarlo mejor:
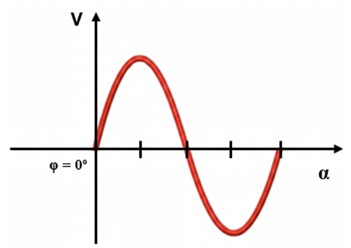
● Fase φ = 0º (0 rad): v (0) = Vmáx · sen (0º) = 0. La onda parte del origen.
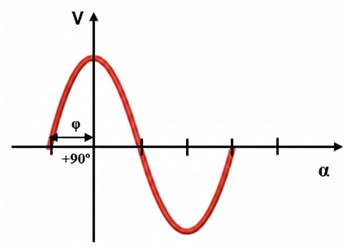
● Fase φ = 90º (π/2 rad): v (0) = Vmáx · sen (90º) = Vmáx · 1 = Vmáx. La onda comienza ya en su valor máximo positivo. La onda está desplazada hacia la izquierda. El cruce por cero ocurrió antes de nuestro tiempo cero. La onda está adelantada respecto al origen. El ángulo φ es positivo (+φ).
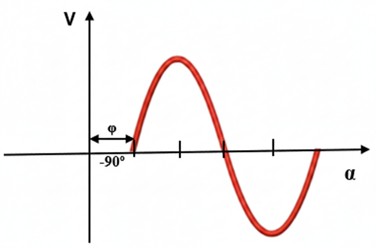
● Fase φ = -90º (-π/2 rad): v (0) = Vmáx · sen (-90º) = Vmáx · (-1) = - Vmáx. La onda comienza ya en su valor máximo negativo. La onda está desplazada hacia la derecha. El cruce por cero ocurrirá después de nuestro tiempo cero. La onda está atrasada respecto al origen. El ángulo φ es negativo (-φ).
Entender este parámetro individual es indispensable para comprender el desfase entre 2 ondas.
Desfase (φ): Ángulo entre Dos Ondas
Si el ángulo de fase (φ) es la posición de una sola onda, el desfase es la relación relativa entre 2 ondas que tienen la misma frecuencia. En el análisis de circuitos de potencia, comparamos casi exclusivamente 2 ondas: la onda de Voltaje (v) y la onda de Corriente (i).
El desfase responde a una pregunta simple: ¿Ocurren los picos de voltaje y corriente al mismo tiempo?
El desfase (φ) es la diferencia angular entre el cruce por cero (o el pico) de la onda de voltaje y el cruce por cero de la onda de corriente.
Matemáticamente, es la resta de sus fases individuales:
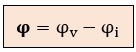
En la práctica, se asume la onda de voltaje v(t) se suele usar como la referencia.
Dependiendo de los componentes del circuito (resistencias, bobinas o condensadores), esta relación cambia totalmente, dando lugar a 3 escenarios fundamentales:
En Fase: El Circuito Resistivo Puro
En un circuito compuesto solo por resistencias (como estufas eléctricas, bombillas incandescentes o planchas), la electricidad fluye sin obstrucción reactiva.
La corriente responde instantáneamente al voltaje. Cuando el voltaje sube, la corriente sube. Cuando el voltaje es cero, la corriente es cero. El desfase es nulo (0º o 0 rad).
La implicación es que toda la energía extraída de la red se convierte en trabajo útil (calor o luz).
Si superponemos las gráficas, ambas ondas cruzan el eje horizontal exactamente en los mismos puntos. "Caminan de la mano".
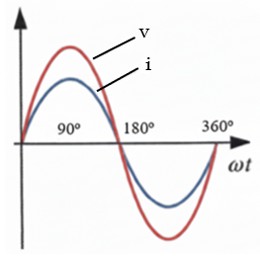
Corriente en Atraso: El Circuito Inductivo
Este es el escenario más común en la industria, ya que la mayoría de las cargas son inductivas (motores, transformadores, relés).
Las bobinas se oponen a los cambios de corriente debido a la Ley de Lenz, almacenando energía en un campo magnético. Esta "inercia magnética" hace que la corriente tarde en reaccionar.
Primero aplicamos el voltaje, y la corriente "tarda" en empezar a fluir con fuerza. La onda de corriente alcanza su pico después que la onda de voltaje. Se dice que "la corriente atrasa al voltaje" (lagging).
El ángulo φ es negativo (< 0º).
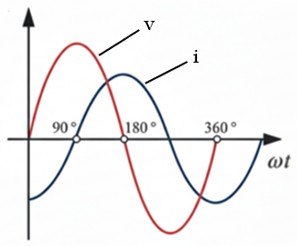
Corriente en Adelanto: El Circuito Capacitivo
Ocurre cuando predominan los condensadores (capacitores). Es menos común como carga natural, pero se usa intencionalmente para corregir problemas en la red.
Un condensador funciona almacenando carga en un campo eléctrico. Para que exista voltaje entre sus placas, primero deben fluir electrones para cargarlas.
La corriente debe fluir antes de que el voltaje pueda acumularse. La onda de corriente alcanza su pico antes que la onda de voltaje. Se dice que "la corriente adelanta al voltaje" (leading).
El ángulo φ es positivo (> 0º).

Importancia del Desfase para el Factor de Potencia
Entender el desfase no es un ejercicio académico; es la base de la eficiencia energética. El ángulo de desfase φ determina directamente el Factor de Potencia (FP) o cos φ:
– Si φ = 0º (resistivo): cos (0º) = 1. Factor de Potencia unitario (Perfecto). Toda la corriente se usa para trabajar.
– Si φ es grande (inductivo/capacitivo): el coseno disminuye (p.ej., 0,8 o 0,5).
¿Por qué importa? Cuando hay desfase (cuando V e I no están alineados), el circuito consume más corriente de la necesaria para realizar el mismo trabajo. Aparece la potencia reactiva (Q), que es energía que va y viene entre el generador y la carga magnética sin hacer trabajo útil real, pero ocupando espacio en los cables.
Esto obliga a las compañías eléctricas a sobredimensionar sus cables y transformadores. Por eso, las industrias pagan penalizaciones si su desfase es muy grande (Factor de Potencia bajo), y deben instalar "bancos de condensadores" (adelanto) para contrarrestar a sus motores (atraso) y reducir el ángulo φ a cero.
También te puede interesar:

Condensador Eléctrico (Capacitor): Qué es, Tipos, Código y Fórmulas
Bobina o Inductor Eléctrico: Qué es, Símbolo y Funcionamiento (Ley de Lenz)
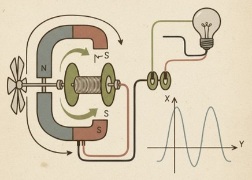
Generación de Corriente Alterna: El Alternador y la Inducción Electromagnética
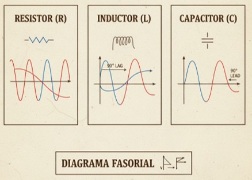
Receptores en Corriente Alterna: Circuitos R, L y C (Resistivo, Inductivo y Capacitivo)
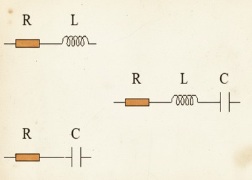
Circuitos Serie RL, RC y RLC: Impedancia, Fórmulas y Resonancia

Receptores en Paralelo (RLC): Cálculo de Corrientes y Potencias
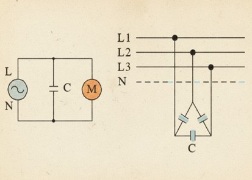
Factor de Potencia (cos φ) y Energía Reactiva: Qué es y Cómo Corregirlo
Conexión Estrella y Triángulo: Diferencias, Esquemas y Voltajes (230/400V)