Receptores en Corriente Alterna: Circuitos R, L y C (Resistivo, Inductivo y Capacitivo)
En Corriente Continua, una bobina es simplemente un cable enrollado y un condensador es un corte en el circuito. Pero cuando conectamos estos componentes a la Corriente Alterna, su comportamiento cambia radicalmente.
Aquí entra en juego la frecuencia: las bobinas se vuelven 'pesadas' (inercia inductiva) y los condensadores actúan como 'muelles' (elasticidad capacitiva).
En esta guía analizaremos por separado los tres tipos de receptores fundamentales (Resistivo, Inductivo y Capacitivo), explicando cómo cada uno provoca un desfase diferente entre la tensión y la corriente, dando lugar a los conceptos de Reactancia (X) e Impedancia (Z).
A diferencia de la corriente continua (CC), donde el flujo de electrones es constante y unidireccional, la corriente alterna (CA) es un entorno dinámico. Aquí, la tensión y la intensidad oscilan, cambian de polaridad constantemente (generalmente 100 o 120 veces por segundo).
Esto provoca que los componentes eléctricos reaccionen de formas muy distintas a como lo harían en un circuito de baterías.
Contenidos
- Componentes Reales vs Componentes Puros (Ideales)
- Resistencia (R) vs Reactancia (X): El freno real y el imaginario
- Circuito Resistivo Puro (En Fase)
- Circuito Inductivo Puro (La Bobina Frena Retrasando)
- Circuito Capacitivo Puro (El Condensador Frena Cargando)
- Cuadro Resumen Comparativo
- Conceptos Transversales Importantes
Componentes Reales vs Componentes Puros (Ideales)
En el mundo real, ningún componente es perfecto:
– Una resistencia puede tener una mínima inductancia si está bobinada.
– Una bobina de cobre tiene resistencia propia (porque el cable tiene longitud).
– Un condensador tiene pequeñas fugas de corriente.
Sin embargo, para aprender electricidad y deducir las fórmulas matemáticas, utilizamos la abstracción del receptor ideal. En este tema asumiremos que los componentes son "puros":
– Una resistencia pura no crea campos magnéticos.
– Una inductancia pura (bobina) no tiene resistencia óhmica (0 Ω de resistencia del cable).
– Un capacitor puro (condensador) tiene una resistencia de aislamiento infinita.
Esta simplificación nos permite aislar y analizar el fenómeno físico único que aporta cada elemento al circuito de corriente alterna.
Resistencia (R) vs Reactancia (X): El freno real y el imaginario
Las 3 magnitudes fundamentales que determinan la oposición al flujo de corriente son la resistencia (R), la inductancia (L) y la capacidad (C). Cada una presenta un tipo de oposición distinto al paso de la corriente eléctrica.
La propiedad que define la oposición de la inductancia y capacidad a la corriente alterna se conoce genéricamente como reactancia (X). Esta se clasifica según el elemento: reactancia inductiva (XL) para las bobinas y reactancia capacitiva (XC) para los condensadores.
La impedancia (Z) es el concepto que unifica estas 3 magnitudes en el análisis de circuitos de CA. Representa la oposición total al flujo de corriente, combinando tanto la resistencia como la reactancia (inductancia y capacidad). La impedancia nos permite tratar circuitos de CA de manera similar a como tratamos circuitos de CC con la ley de Ohm.
Resistencia (R)
Es la oposición al paso de la corriente mediante la fricción de los electrones a nivel atómico. La resistencia convierte la energía eléctrica irreversiblemente en calor (Efecto Joule). Su unidad es el Ω. El símbolo se representa comúnmente como un zig-zag o un rectángulo.
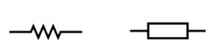
Es el freno real de la corriente porque la energía que se opone aquí se pierde definitivamente del circuito y no produce desfase entre la tensión y la corriente.
Inductancia (L)
Es la propiedad de almacenar energía en forma de campo magnético. Generalmente se consigue mediante una bobina o solenoide, enrollando un conductor.
La bobina se opone a los cambios en la corriente. Actúa como una "inercia" eléctrica; a la corriente le cuesta arrancar y le cuesta frenar. Su unidad es el Henrio (H). El símbolo se representa así:
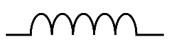
Es el freno imaginario de la corriente, siendo una oposición basada en la creación de campos magnéticos que almacenan temporalmente la energía eléctrica y luego la devuelven al circuito.
La oposición a la corriente que provocan las bobinas se denomina reactancia inductiva (XL), produciendo un desfase de +90° (la corriente se atrasa respecto al voltaje).
Capacidad (C)
Es la propiedad de almacenar energía en forma de campo eléctrico entre 2 placas conductoras separadas por un aislante (dieléctrico). El componente con esta propiedad es el condensador.
El condensador se opone a los cambios en la tensión. Actúa como un "muelle" o tanque elástico; se carga y descarga devolviendo la energía al circuito. Su unidad es el Faradio (F). Su símbolo es el siguiente:
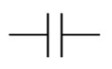
Constituye también un freno imaginario de la corriente, siendo una oposición basada en la creación de campos eléctricos que almacenan temporalmente la energía eléctrica para devolverla posteriormente al circuito.
La oposición a la corriente que provocan los condensadores se denomina reactancia capacitiva (XC), produciendo un desfase de -90° (la corriente se adelanta respecto al voltaje).
Influencia de la Frecuencia
Por otro lado, el comportamiento de los circuitos con bobina (L) o con condensador (C) depende totalmente de la frecuencia (f), medida en Hercios (Hz). La frecuencia indica la rapidez con la que la corriente cambia de sentido. Si la frecuencia cambia, la oposición que ofrecen estos componentes (llamada reactancia) cambia drásticamente.
En cambio, para la resistencia (R), la frecuencia es indiferente. Una estufa eléctrica de 1000 Ω calentará igual si la conectamos a una batería (CC), a la red de 50 Hz o a una red de 400 Hz. Su oposición es constante.
Circuito Resistivo Puro (En Fase)
El elemento más básico y fácil de comprender en un circuito de corriente alterna es la resistencia pura. De los 3 receptores en corriente alterna pasivos, la resistencia es el único componente cuyo comportamiento es similar al que presenta en corriente continua, aunque adaptado a la naturaleza oscilatoria de la señal.
Desde el punto de vista físico, una resistencia pura es un componente pasivo que se opone al paso de la corriente eléctrica mediante la "fricción" de los electrones contra la estructura atómica del material conductor.
A diferencia de las bobinas o condensadores, la resistencia no almacena energía. Toda la energía eléctrica que recibe la transforma inmediata e irreversiblemente en calor. Este fenómeno se conoce como Efecto Joule.
Por ejemplo, las resistencias de un radiador eléctrico, la de una plancha de ropa o la del filamento de una bombilla incandescente.

Tensión e Intensidad de una Resistencia en Corriente Alterna
Lo que define a una carga resistiva pura en corriente alterna es la instantaneidad de su respuesta. La resistencia no tiene "inercia" magnética ni eléctrica.
Si aplicamos una tensión alterna a una resistencia:
- En el instante en que la tensión es máxima, la corriente es máxima.
- En el instante en que la tensión es cero, la corriente es cero.
- Cuando la tensión invierte su polaridad, la corriente cambia de sentido al mismo tiempo.
Decimos coloquialmente que la onda de Tensión (V) y la onda de Intensidad (I) van "de la mano".
En electricidad, el desfase (φ) es el ángulo de separación temporal entre la onda de tensión y la de corriente. Debido a la sincronización perfecta explicada anteriormente, en un circuito puramente resistivo no existe desfase.
En un circuito de receptores en corriente alterna resistivo puro, la intensidad y la tensión están en fase: φ = 0º. Esto significa que ambas ondas cruzan por el eje horizontal (punto cero) exactamente en el mismo instante, tal como se observa en la gráfica de ondas o diagrama senoidal.
Ley de Ohm para una Resistencia en Corriente Alterna
Dado que no hay desfases ni fenómenos complejos de almacenamiento de energía, la relación matemática entre tensión e intensidad se rige por la Ley de Ohm, exactamente igual que en corriente continua, pero utilizando valores eficaces (RMS).
La fórmula fundamental es:

donde:
I = intensidad eficaz en Amperios (A).
V = tensión eficaz en Voltios (V).
R = resistencia eléctrica en Ohmios (Ω).
Esta resistencia óhmica (R) no varía con la frecuencia. Por ejemplo, una resistencia de 100 Ω a 50 Hz sigue siendo de 100 Ω a 1000 Hz.
Potencia de una Resistencia en Corriente Alterna
En los circuitos con receptores en corriente alterna existen 3 tipos de potencia (activa, reactiva y aparente). Las resistencias son las únicas responsables de consumir la potencia activa (P), que es la potencia "útil" que se transforma en trabajo real (calor, luz, etc.).
La fórmula general de la potencia en monofásica es P = V · I · cos φ. Como sabemos que en una resistencia el ángulo es φ = 0º, y el coseno de 0 es 1 (cos 0º = 1), la fórmula se simplifica a su máxima expresión:

También podemos expresarla sustituyendo según la Ley de Ohm:


La unidad de la potencia activa se mide en Vatios (W).
Diagrama Vectorial de un Circuito con Resistencia
Mientras que el diagrama senoidal muestra el movimiento continuo de las ondas, el diagrama vectorial muestra la relación de posición en un momento concreto.
Un diagrama vectorial o fasorial, es una representación gráfica estática que captura la magnitud y la relación de fase entre las diferentes tensiones y corrientes en un instante específico del tiempo. No representa el movimiento de rotación de los vectores.
El diagrama vectorial tradicional es una imagen fija que nos permite visualizar y calcular de forma inmediata los desfases. Este diagrama nos muestra quién va adelantado y quién va retrasado en un circuito con receptores en corriente alterna.
Este diagrama utiliza fasores (vectores rotatorios) para representar la tensión y la corriente.
En el caso de la resistencia:
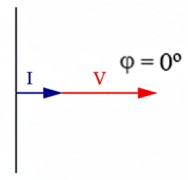
- Dibujamos el vector de tensión (V) generalmente en el eje horizontal de referencia (0º).
- Como no hay desfase, el vector de intensidad (I) se dibuja superpuesto al de tensión, con la misma dirección y sentido.
Visualmente, ambos vectores apuntan a la misma dirección, lo que confirma gráficamente que el ángulo entre ellos es cero, φ = 0º.
Circuito Inductivo Puro (La Bobina Frena Retrasando)
Tras analizar la resistencia, entramos en el terreno de los componentes que almacenan energía. El primero de ellos es la inductancia, físicamente materializada en forma de bobina (un conductor enrollado en espiral, a veces sobre un núcleo de hierro).

Una bobina ideal no tiene resistencia óhmica (R = 0 Ω). Su propiedad fundamental es que, al pasar una corriente por ella, genera un campo magnético a su alrededor.
El principio físico clave aquí es la autoinducción (Ley de Lenz): "La bobina induce una tensión que se opone a la causa que la produce".
Esto significa que la bobina se opone a los cambios de corriente.
– Si la corriente intenta aumentar, la bobina genera una fuerza inversa para frenarla.
– Si la corriente intenta disminuir, la bobina devuelve energía para intentar mantenerla.
Podemos pensar en la bobina como una "inercia eléctrica"; a la corriente le cuesta arrancar y le cuesta detenerse.
Concepto de Reactancia Inductiva
En corriente alterna, como la corriente está cambiando constantemente de valor y sentido, la bobina está constantemente oponiéndose a esos cambios. Esta oposición continua no disipa calor, pero limita el paso de la corriente. A esta "resistencia magnética" la llamamos reactancia inductiva (XL).
A diferencia de la resistencia, la reactancia inductiva depende directamente de la frecuencia, es decir, de la rapidez de los cambios:
– Baja frecuencia: la corriente cambia despacio. La bobina se opone poco (XL baja).
– Alta frecuencia: la corriente intenta cambiar muy rápido. La bobina reacciona violentamente oponiéndose mucho (XL alta).
El valor en Ohmios de esta oposición se calcula mediante esta fórmula de la reactancia inductiva:
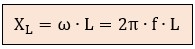
donde:
XL = se mide en Ohmios (Ω).
ω = velocidad angular en radianes por segundo (rad/s).
f = frecuencia en Hercios (Hz).
L = inductancia en Henrios (H).
Según la fórmula de la reactancia inductiva, a mayor frecuencia, mayor oposición. Una bobina "frena" más las señales de alta frecuencia (como un filtro de graves que deja pasar los sonidos bajos).
Tensión e Intensidad de una Bobina en Corriente Alterna
Debido a esa inercia magnética explicada anteriormente, la corriente tarda un tiempo en establecerse después de aplicar la tensión.
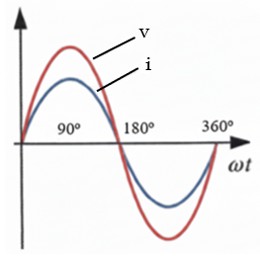
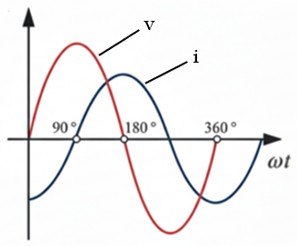
En una bobina pura, la intensidad se retrasa 90º respecto a la tensión.
Esto significa que la tensión alcanza su valor máximo primero, y la corriente lo alcanza un cuarto de ciclo después. Matemáticamente, decimos que hay un desfase de φ = +90º (o π/2 radianes) inductivos.
Si tomamos la tensión como referencia, los valores instantáneos de tensión y corriente son:
- v(t) = Vmáx · sen (ωt)
- i(t) = Imáx · sen (ωt – 90º)
Entonces el desfase, que por definición es la diferencia entre el cruce por cero de la onda de voltaje y el cruce por cero de la onda de corriente (cuánto adelanta la tensión a la corriente), es:
φ = φv – φi = 0º - (-90º) = + 90º
En la siguiente gráfica, se observa cómo la onda de tensión (V) cruza por cero subiendo, y la onda de intensidad (I) no cruza por cero hasta un rato después (90º después).
Ley de Ohm para una Bobina en Corriente Alterna
Para calcular la magnitud de la corriente que circulará por una bobina, adaptamos la Ley de Ohm sustituyendo la resistencia por la reactancia inductiva:
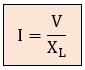
Si desglosamos la fórmula completa, vemos claramente cómo la frecuencia afecta a la corriente:
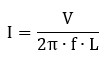
(A mayor frecuencia f, mayor denominador y, por tanto, menor intensidad I).
Potencia de una Bobina en Corriente Alterna
Aquí ocurre algo curioso: aunque circula corriente y hay tensión, la bobina ideal no consume energía. No se calienta.
● Potencia activa (P): es nula. La bobina pura ideal (sin resistencia) no se calienta.
P = V · I · cos φ = V · I · cos (90º) = 0 W.
● Potencia reactiva (QL): la bobina toma energía de la red para crear su campo magnético y, en el siguiente semiciclo, devuelve esa energía a la red al destruir el campo. Es un intercambio constante de "ida y vuelta" que carga las líneas pero no produce trabajo útil.
La potencia reactiva inductiva se calcula como QL = V · I · sen φ. Como en la bobina ideal, sen 90º = 1, la fórmula queda:
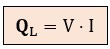
La unidad de la potencia reactica es el Voltamperio Reactivo (VAr).
Si sustituimos la Ley de Ohm en esta fórmula básica de la potencia reactiva QL, obtenemos 2 expresiones alternativas:
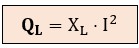
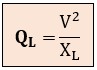
Diagrama Vectorial de un Circuito con Bobina
Para representar esto gráficamente mediante fasores:
- Tomamos la tensión (V) como referencia en el eje horizontal (0º).
- Como la intensidad va con retraso, dibujamos el vector de intensidad (I) girado 90º en sentido horario (hacia abajo).
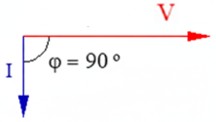
Este vector de intensidad apuntando hacia abajo (-90º o -φ) es la firma inconfundible de un comportamiento inductivo puro.
Nota: No confundir este ángulo de la corriente con el ángulo de desfase φ de +90° desde la perspectiva de cuánto adelanta la tensión a la corriente.
Circuito Capacitivo Puro (El Condensador Frena Cargando)
Si la bobina era la inercia magnética, el condensador (o capacitor) es la elasticidad eléctrica. Es el componente complementario y opuesto a la bobina en casi todos sus aspectos.
Físicamente, un condensador consta de 2 placas conductoras separadas por un material aislante llamado dieléctrico. A diferencia de la resistencia, no hay conexión eléctrica directa entre sus terminales.
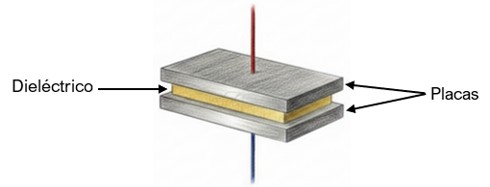
Su función es almacenar energía en forma de campo eléctrico (acumulación de cargas electrostáticas en sus placas).
Funciona como un depósito de gas a presión o un muelle. Para que la presión (tensión) suba, primero debe entrar gas (corriente).
Concepto de Reactancia Capacitiva
En corriente continua, un condensador es un circuito abierto (no pasa corriente una vez cargado). Sin embargo, en corriente alterna, al estar la tensión cambiando de polaridad continuamente, el condensador se carga y descarga sin cesar, permitiendo una circulación de electrones por el circuito exterior.
La oposición que presenta a este proceso de carga y descarga se llama reactancia capacitiva (XC).
Aquí ocurre lo contrario que en la bobina:
– Mayor frecuencia (f): si la polaridad cambia muy rápido, el condensador se carga y descarga velozmente. Ofrece menos oposición (XC baja).
– Mayor capacidad (C): si el "depósito" es más grande, caben más electrones, facilitando el paso de la corriente. Ofrece menos oposición.
La reactancia capacitiva refleja matemáticamente esta relación inversa situando las variables en el denominador:
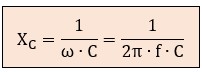
donde:
XC = reactancia capacitiva, en Ohmios (Ω)
ω = velocidad angular, en radianes por segundo (rad/s)
f = frecuencia de la señal AC, en Hercios (Hz)
C = capacidad del condensador, en Faradios (F)
Según la fórmula de la reactancia capacitiva, a mayor frecuencia, menor oposición. Un condensador "deja pasar" mejor las señales de alta frecuencia (como un filtro de agudos que deja pasar los sonidos altos).
Tensión e Intensidad de un Condensador en Corriente Alterna
Para que aparezca tensión (diferencia de potencial) entre las placas de un condensador, primero tienen que llegar las cargas (electrones). Por tanto, la corriente debe fluir antes de que la tensión suba.
En un condensador puro, la intensidad se adelanta 90º respecto a la tensión.
Si tomamos la tensión como referencia, los valores instantáneos de tensión y corriente son:
- v(t) = Vmáx · sen (ωt)
- i(t) = Imáx · sen (ωt + 90º)
Entonces el desfase, que por definición es la diferencia entre el cruce por cero de la onda de voltaje y el cruce por cero de la onda de corriente (cuánto adelanta la tensión a la corriente), es:
φ = φv – φi = 0º - (+90º) = - 90º
En la siguiente gráfica, se observa que la onda de intensidad (I) llega a su pico máximo un cuarto de ciclo antes que la onda de tensión (V). Matemáticamente, decimos que hay un desfase de φ = -90º (o π/2 radianes) capacitivos.

Ley de Ohm para un Condensador en Corriente Alterna
Para calcular la corriente, aplicamos nuevamente la Ley de Ohm sustituyendo la resistencia por la reactancia capacitiva:
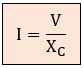
Si desglosamos la fórmula completa, vemos claramente cómo la frecuencia afecta a la corriente:
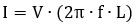
Esta ecuación revela algo muy práctico: la intensidad es directamente proporcional a la frecuencia. A altas frecuencias, un condensador puede comportarse casi como un cortocircuito.
Potencia de un Condensador en Corriente Alterna
Al igual que la bobina, el condensador ideal es un elemento reactivo que no consume energía real.
● Potencia activa (P): es nula. El condensador no se calienta (idealmente).
P = V · I · cos φ = V · I · cos (-90º) = 0 W.
● Potencia reactiva (QL): el condensador almacena energía en el campo eléctrico durante un cuarto de ciclo y la devuelve al circuito en el siguiente.
A menudo se dice que el condensador "genera" potencia reactiva (en contraposición a la bobina que la "consume"), aunque técnicamente es un intercambio. Esto es clave para la corrección del factor de potencia en industrias.
La potencia reactiva capacitiva se calcula como QC = V · I · sen φ. El sen (-90º) = -1, pero si prescindimos del signo negativo, la fórmula queda:

El hecho de que esta potencia QC sea negativa indica precisamente que la carga capacitiva genera o "inyecta" potencia reactiva en el sistema. En cambio, el signo positivo de la potencia QL indica que la carga inductiva consume potencia reactiva.
La unidad de la potencia reactica es el Voltamperio Reactivo (VAr).
Si sustituimos la Ley de Ohm en esta fórmula básica de la potencia reactiva QC, obtenemos 2 expresiones alternativas:
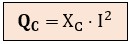
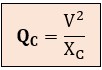
Diagrama Vectorial de un Circuito con Condensador
La representación gráfica es la inversa de la inductancia:
1º) Fijamos la tensión (V) en el eje horizontal (0º).
2º) Como la intensidad se adelanta, dibujamos el vector de intensidad (I) girado 90º en sentido antihorario (hacia arriba).
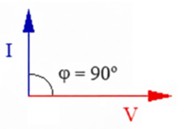
En el plano complejo, este vector de intensidad corresponde al eje imaginario positivo (+90º o +φ).
Nota: No confundir este ángulo de la corriente con el ángulo de desfase φ de -90° desde la perspectiva de cuánto adelanta la tensión a la corriente.
Cuadro Resumen Comparativo
En el análisis de circuitos de corriente alterna, es fácil confundirse entre quién adelanta a quién o qué fórmula depende inversamente de la frecuencia.
La siguiente tabla sintetiza el comportamiento de los 3 receptores elementales puros en corriente alterna (R, L, C) sometidos a una tensión senoidal. Esta es la referencia rápida que todo electricista o estudiante debe tener en mente.
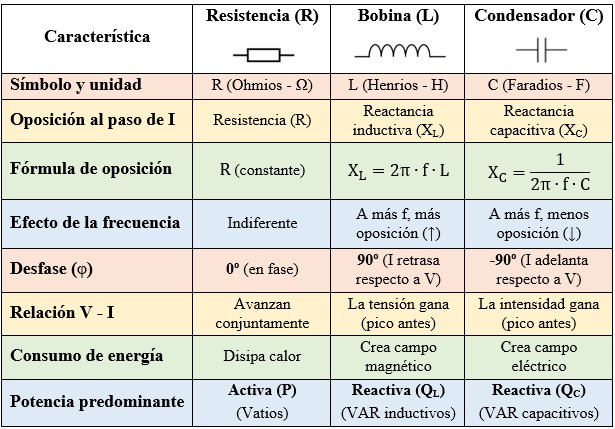
Observando la última fila de la tabla, podemos deducir el comportamiento energético del circuito:
- Tiene una parte resistiva (P) si tocamos un componente y está caliente.
- Es predominantemente inductivo (QL) si el componente vibra o genera campos magnéticos sin calentarse (idealmente).
- Es capacitivo (QC) si el componente almacena carga estática de alto voltaje.
Conceptos Transversales Importantes
Hasta ahora hemos llamado a la oposición de la corriente "Resistencia" o "Reactancia" según el componente. Sin embargo, en el cálculo eléctrico profesional, necesitamos un concepto que englobe a todos ellos para poder operar en circuitos mixtos. Aquí entran en juego dos conceptos gigantes: la impedancia y el factor de potencia.
La Impedancia (Z)
La impedancia (Z) es la magnitud total que se opone al paso de la corriente alterna. Es el concepto "paraguas" que une a la resistencia y a las reactancias. Se mide en Ohmios (Ω).
● La Ley de Ohm universal: gracias a la impedancia, podemos escribir una sola fórmula que sirve para cualquier circuito de CA, sea cual sea su componente:
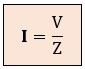
● ¿Cuánto vale Z en nuestros receptores puros?: Como aquí estamos analizando componentes ideales por separado, la impedancia toma el valor exacto de la única oposición presente:
- En un circuito resistivo puro: Z = R (la impedancia es puramente resistiva).
- En un circuito inductivo puro: Z = XL (la impedancia es puramente reactiva inductiva).
- En un circuito capacitivo puro: Z = XC (la impedancia es puramente reactiva capacitiva).
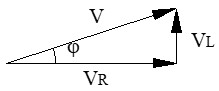
🔍 Nota: cuando estudiemos circuitos serie (ej. una bobina con una resistencia), la impedancia (Z) será la suma vectorial de ambas (R y XL), formando el famoso "Triángulo de impedancias". Pero en receptores puros, Z es igual al componente único que existe.
El Factor de Potencia (cos φ)
El Factor de Potencia (FP o cos φ) es un indicador de calidad que nos dice qué porcentaje de la energía que circula se está transformando realmente en trabajo útil (calor, luz, movimiento, etc.).
Matemáticamente, es el coseno del ángulo de desfase (φ) que vimos en los puntos anteriores. Su valor oscila entre 0 y 1.
● En la resistencia (el caso ideal): como la tensión e intensidad están en fase (φ = 0), el factor de potencia FP = cos 0º = 1. El 100% de la energía absorbida se aprovecha. Es el escenario ideal para la compañía eléctrica.
● En bobinas y condensadores puros (el caso pésimo): como la tensión e intensidad están desfasadas 90º (φ = +90º o φ = -90º), el rendimiento es nulo. Esto es físicamente muy importante: por los cables circula corriente (y mucha), los cables se calientan y los transformadores trabajan, pero no se produce potencia útil (P = 0 W).
Implicación práctica: un circuito con un cos φ bajo (cercano a 0) es muy ineficiente. Obliga a la compañía eléctrica a transportar mucha corriente "gratis" que solo entra y sale de las bobinas/condensadores sin hacer trabajo. Por eso, en la industria se penaliza el mal factor de potencia y se instalan baterías de condensadores para corregirlo.
Conclusión y Siguientes Pasos
Hemos desglosado la "personalidad" única de los 3 receptores elementales en corriente alterna:
● La resistencia (R): es la trabajadora incansable. Disipa energía y mantiene V e I unidos.
● La bobina (L): es la inercia magnética. Se opone a los cambios de corriente y la retrasa.
● El condensador (C): es el muelle eléctrico. Se opone a los cambios de tensión y provoca que la corriente se adelante.
En el mundo real, rara vez encontramos una bobina o un condensador aislados. Lo normal es encontrar motores (bobinas con resistencia interna) o redes complejas. El siguiente paso natural en el procedimiento de aprendizaje es combinar estos elementos. En las próximas secciones analizaremos:
– Circuitos serie R-L: cómo la resistencia y la bobina "pelean" por el ángulo de desfase.
– Circuitos serie R-C y R-L-C: el análisis vectorial completo y el fenómeno de la resonancia.
Visualización final: Debemos recordar que R está en el eje real, L en el imaginario positivo y C en el imaginario negativo. Esta suele ser la base de los diagramas complejos. Por ejemplo, en un circuito serie los vectores del voltaje en la resistencia y en la bobina se representarían así:
También te puede interesar:

Condensador Eléctrico (Capacitor): Qué es, Tipos, Código y Fórmulas
Bobina o Inductor Eléctrico: Qué es, Símbolo y Funcionamiento (Ley de Lenz)
Generación de Corriente Alterna: El Alternador y la Inducción Electromagnética
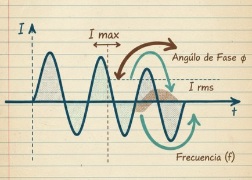
Parámetros de la Onda Senoidal (CA): Frecuencia, Periodo y Valor Eficaz (RMS)
Circuitos Serie RL, RC y RLC: Impedancia, Fórmulas y Resonancia

Receptores en Paralelo (RLC): Cálculo de Corrientes y Potencias
Factor de Potencia (cos φ) y Energía Reactiva: Qué es y Cómo Corregirlo
Conexión Estrella y Triángulo: Diferencias, Esquemas y Voltajes (230/400V)