Circuitos Serie RL, RC y RLC: Impedancia, Fórmulas y Resonancia
En Corriente Continua, sumar componentes en serie es tan fácil como una suma aritmética. Sin embargo, en Corriente Alterna, las reglas cambian. Aquí no podemos sumar directamente los Ohmios de una resistencia con los de una bobina, porque actúan en tiempos diferentes (desfase).
Para resolver estos circuitos (RL, RC y RLC), necesitamos utilizar el Triángulo de Impedancias y la suma vectorial.
En esta guía aprenderás a calcular la Impedancia Total (Z), determinar el ángulo de desfase (φ) y entender el peligroso fenómeno de la Resonancia Serie, donde las fuerzas inductivas y capacitivas se anulan mutuamente.
El objetivo central es proporcionar una introducción detallada a los circuitos serie alimentados por corriente alterna, explorando de manera sistemática las diferentes combinaciones posibles entre R, L y C.
Para estudios básicos o conceptuales, como es nuestro caso, se puede prescindir de los números complejos usando métodos gráficos o trigonométricos. No obstante, en ingeniería aplicada, diseño o análisis avanzado, los números complejos son imprescindibles.
Contenidos
- Definición Básica del Circuito Serie
- Conceptos Previos: Resistencia, Reactancia e Impedancia
- El Circuito Serie RL (Resistencia – Bobina)
- El Circuito Serie RC (Resistencia – Condensador)
- El Circuito Completo (RLC): Restando Reactancias
- Potencias en los Receptores Monofásicos en Serie
- Ejercicios Resueltos de Circuitos serie RL, RC y RLC
- La Resonancia Serie: Cuando XL anula a XC
Definición Básica del Circuito Serie
Un circuito serie se define por la forma en que los componentes pasivos resistencias (R), bobinas (L) y condensadores (C) están interconectados. En esta configuración, los elementos se disponen uno a continuación del otro, formando un único camino cerrado para el flujo de electrones.
No existen nudos ni derivaciones. Esto significa que la energía suministrada por la fuente de tensión alterna debe atravesar obligatoriamente cada uno de los componentes secuencialmente para cerrar el circuito.
El Comportamiento de la Intensidad en el Circuito Serie
Si hay un concepto que debemos grabar a fuego para resolver cualquier ejercicio de receptores monofásicos en serie, es este: En un circuito serie, la Intensidad (I) es única y común a todos los componentes.
Dado que solo existe un camino físico, la cantidad de carga eléctrica que pasa por la resistencia en un segundo es exactamente la misma que pasa por la bobina y el condensador en ese mismo instante. No importa el valor de los componentes; la corriente no se "gasta" ni se pierde, simplemente circula.
Matemáticamente, esto se expresa como: IT = IR = IL = IC.
Debido a esta propiedad, cuando dibujamos los diagramas fasoriales (representaciones gráficas de vectores rotatorios), siempre utilizamos la intensidad como vector de referencia (se dibuja en el eje horizontal a 0º), ya que es el único valor constante en todo el sistema.
El Comportamiento de la Tensión en el Circuito Serie
Aquí es donde la mayoría de los estudiantes de electricidad encuentran su primer obstáculo.
En un circuito de corriente continua (CC) con varias resistencias en serie, la tensión total de la fuente se reparte proporcionalmente. Si sumamos la caída de tensión en cada resistencia, obtenemos el voltaje de la pila: VT = V1 + V2 + V3 … (solo válido en CC).
Sin embargo, en corriente alterna esto NO suele cumplirse aritméticamente.
Si tomamos un voltímetro y medimos las caídas de tensión en una resistencia, una bobina y un condensador conectados en serie, y luego sumamos esos valores directamente, el resultado será casi siempre mayor que la tensión que está suministrando el generador.
¿Por qué ocurre esto? (introducción a los fasores) en CA, las bobinas y los condensadores no solo se oponen al paso de la corriente, sino que desfasan la onda de tensión respecto a la de intensidad:
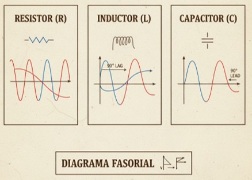
– Resistencia (R): la tensión e intensidad van a la par (en fase).
– Bobina (L): la tensión se adelanta 90º a la corriente.
– Condensador (C): la tensión se retrasa 90º respecto a la corriente.
Debido a estos desfases temporales, los picos máximos de voltaje en la bobina no ocurren al mismo tiempo que los picos en la resistencia. Por tanto, no podemos sumar sus valores como números normales (escalares); debemos sumarlos como vectores (fasores).
La Ley de Kirchhoff de los voltajes sigue siendo válida, pero en su forma vectorial:
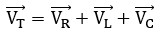
Para calcular la magnitud real (el valor eficaz que mediría un voltímetro en la entrada), tendremos que utilizar el Teorema de Pitágoras, dando lugar a las fórmulas de impedancia que veremos en los siguientes apartados.
Conceptos Previos: Resistencia, Reactancia e Impedancia
Para analizar circuitos R-L, R-C o R-L-C sin perderse en las matemáticas, primero debemos entender la naturaleza de los "obstáculos" que la electricidad encuentra a su paso. En corriente alterna (CA), la oposición al paso de la corriente no es siempre igual: puede ser resistiva (fricción) o reactiva (inercia).
A continuación, desglosamos los 3 parámetros fundamentales que determinan el comportamiento del circuito.
La Resistencia
La resistencia eléctrica es el concepto más familiar. Representa la oposición física que ofrece el material conductor al paso de los electrones debido a los choques de estos con los átomos del material.
La energía eléctrica perdida en la resistencia no desaparece, se transforma irreversiblemente en calor (Efecto Joule). Por eso decimos que es la parte del circuito que consume Potencia Activa.
El valor óhmico de una resistencia ideal no cambia con la frecuencia. Una resistencia de 10 Ω vale lo mismo a 50 Hz que a 1 kHz.
En una resistencia pura, la tensión y la intensidad van perfectamente sincronizadas. El desfase φ = 0. Esto significa que cuando la onda de tensión alcanza su máximo, la intensidad también lo hace.
La Reactancia Inductiva
Cuando una corriente alterna circula por una bobina (inductancia L), crea un campo magnético variable. Según la Ley de Lenz, este campo variable induce una fuerza contraelectromotriz que se opone a los cambios de corriente. Esta oposición no es por rozamiento, es una "inercia magnética".
A esta oposición la llamamos reactancia inductiva (XL) y se mide en Ohmios (Ω).
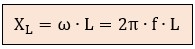
donde:
f = frecuencia de la red en Hercios (Hz)
L = coeficiente de autoinducción en Henrios (H)
ω = pulsación angular (2π · f)
Se observa que XL es directamente proporcional a la frecuencia:
– Si la frecuencia es baja (o cero, como en CC): la bobina apenas opone resistencia (↓XL) y se comporta como un cortocircuito.
– Si la frecuencia es muy alta: la bobina se opone enormemente al paso de la corriente (↑XL).
En una bobina ideal, la corriente siempre va “un paso por detrás” de la tensión, retrasándose exactamente 90 grados. Visualmente, mientras la tensión en sus bornes alcanza su pico máximo, la intensidad aún está en cero, llegando a su propio máximo un cuarto de ciclo más tarde. Esta relación temporal se cuantifica como un desfase de φ = +90º (o π/2 radianes) inductivos.
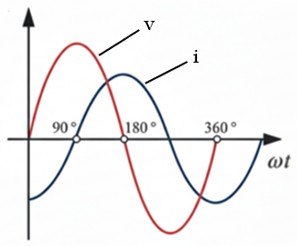
La Ley de Ohm puede aplicarse a la reactancia inductiva de la bobina:
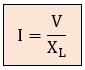
Esto nos permite calcular fácilmente la caída de tensión que provoca la inductancia de la bobina en el circuito serie, que sería: VL = XL · I.
La Reactancia Capacitiva
Un condensador (capacidad C) almacena energía en forma de campo eléctrico. En corriente alterna, el condensador se carga y descarga continuamente. La "reactancia capacitiva" (XC) es la medida de cuánto le cuesta al circuito realizar este proceso de carga y descarga.
La reactancia capacitiva (XC) se mide en Ohmios (Ω).
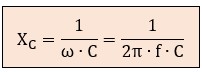
donde:
f = frecuencia en Hercios (Hz)
C = capacidad en Faradios (F)
ω = pulsación angular (2π · f)
Se observa que XC es inversamente proporcional a la frecuencia.
– Si la frecuencia es muy alta: el condensador se carga y descarga rapidísimo, ofreciendo casi nula oposición (↓XC).
– Si la frecuencia es cero (CC): la reactancia es infinita (↑XC) y el condensador se comporta como un circuito abierto (no deja pasar la corriente continua).
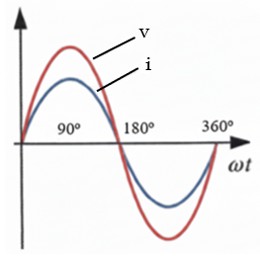
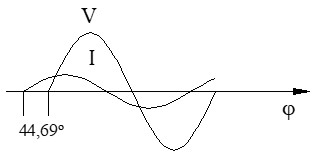
En un condensador ideal, la corriente siempre se anticipa a la tensión, adelantándose exactamente 90 grados. Como muestra la gráfica, la onda de intensidad (I) alcanza su valor máximo un cuarto de ciclo completo antes que la onda de tensión (V). Esta relación temporal se cuantifica como un desfase de φ = -90º (o π/2 radianes) capacitivos.

Del mismo modo, la Ley de Ohm puede aplicarse a la reactancia capacitiva del condensador:
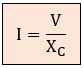
Esto nos permite calcular fácilmente la caída de tensión que provoca la capacidad del condensador en el circuito serie, que sería: VC = XC · I.
La Impedancia (El Triángulo de Impedancias)
En un circuito serie donde coexisten resistencias y reactancias (bobinas o condensadores), no podemos simplemente sumar sus valores en ohmios, porque actúan en "tiempos" diferentes (debido al desfase de 90º de las reactancias).
La impedancia (Z) es la suma vectorial de la resistencia (parte real) y la reactancia (parte imaginaria). Representa la oposición total real que ofrece el circuito conjunto al paso de la corriente alterna. Se mide en Ohmios (Ω).
La Ley de Ohm generalizada nos permite calcular la corriente total del circuito:
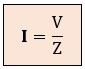
Para calcular el módulo de la impedancia (Z), recurrimos a una herramienta geométrica: el Triángulo de Impedancias.
En él, la componente resistiva (R) se sitúa en el eje horizontal, y la componente reactiva (X) en el vertical. La aplicación del Teorema de Pitágoras nos da el valor de Z.
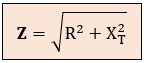
Este resultado no es un número abstracto; es la cantidad que, aplicada en la ley de Ohm (I = V/Z), nos dirá exactamente cuántos amperios circularán por nuestro circuito.
🔍 Nota: la impedancia (Z) se construye geométricamente como la hipotenusa de un triángulo rectángulo cuyos catetos son la resistencia (R) en el eje horizontal y la reactancia (X) en el eje vertical. Dado que estos dos efectos, disipación y almacenamiento de energía, ocurren con 90° de diferencia, no pueden sumarse aritméticamente, sino vectorialmente.
El Circuito Serie RL (Resistencia – Bobina)
El circuito serie R-L es, con diferencia, el modelo más común en el mundo real. Casi cualquier dispositivo que utilice bobinado de cobre para crear campos magnéticos (como el motor de una lavadora, un taladro o un transformador industrial) posee intrínsecamente 2 características:
– Resistencia (R): la propia resistencia del hilo de cobre.
– Inductancia (L): la capacidad de generar campo magnético al estar enrollado.
Por tanto, entender este circuito es entender cómo funcionan la mayoría de las máquinas eléctricas.
Esquema Eléctrico y Conexión
En este circuito, conectamos una resistencia pura en serie con una bobina ideal.
– La intensidad (I): fluye primero por la resistencia y luego atraviesa la bobina (o viceversa, el orden no altera el producto en serie).
– La tensión total (V) aplicada: se reparte entre ambos componentes, creando 2 caídas de tensión distintas: VR y VL.
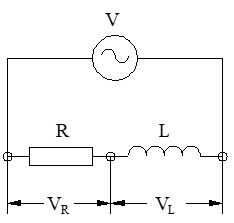
Comportamiento Fasorial
Para analizar qué ocurre con los voltajes, debemos recordar nuestra referencia: la intensidad (I), que dibujamos horizontalmente (0º).
● En la resistencia (VR): la tensión no sufre desfase. El vector VR se dibuja sobre el eje horizontal, en la misma dirección que la intensidad.
● En la bobina (VL): la bobina se opone a los cambios de corriente, provocando que la intensidad se retrase. Dicho de otra forma: la tensión en la bobina adelanta 90º a la intensidad. El vector VL se dibuja vertical hacia arriba.
Al sumar estos 2 vectores (VR horizontal y VL vertical), obtenemos el vector de tensión total (V), que forma la hipotenusa de un triángulo rectángulo.
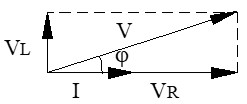
Cálculos en el Circuito Serie RL
Basándonos en la geometría del triángulo formado por los vectores, aplicamos el Teorema de Pitágoras para obtener las magnitudes escalares.
● Tensión total (V): en la práctica, para calcular la tensión que debe suministrar la fuente en un circuito R-L, construimos el triángulo de tensiones.
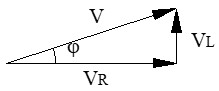
No podemos sumar VR + VL aritméticamente. La tensión real de la fuente es la suma vectorial:
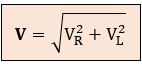
● Impedancia total (Z): si dividimos los lados del triángulo de tensiones por la intensidad (I), obtenemos el triángulo de impedancias.
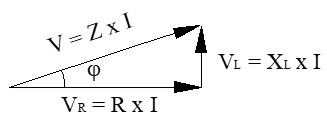
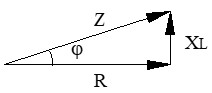
Aquí, la hipotenusa representa la oposición total (Z):
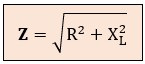
donde:
R = resistencia en Ohmios (Ω).
XL = reactancia inductiva (2π · f · L) en Ohmios (Ω).
Z = impedancia total en Ohmios (Ω).
El Ángulo de Desfase
El ángulo φ (fi) es el desfase que existe entre la tensión total suministrada y la intensidad que circula. En un circuito R-L, este ángulo siempre será positivo (entre 0º y 90º).
Podemos calcularlo usando trigonometría básica en el triángulo de impedancias (tangente = cateto opuesto / contiguo):
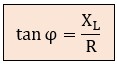
Con lo cual, el desfase φ será:
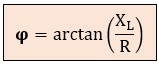
También podríamos usar los voltajes del triángulo de tensiones:
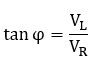
La interpretación física es la siguiente:
– Si R es muy grande comparada con XL: el ángulo será pequeño (cercano a 0º). El circuito es casi resistivo.
– Si XL es muy grande comparada con R: el ángulo será grande (cercano a 90º). El circuito es muy inductivo.
Conclusión: en un circuito R-L, decimos que la intensidad va con retraso respecto a la tensión total. Este "retraso" es el causante de un bajo Factor de Potencia en las industrias.
El Circuito Serie RC (Resistencia – Condensador)
Mientras que el circuito R-L representaba la mayoría de las cargas industriales (motores, bobinas, etc.), el circuito R-C tiene una aplicación diferente pero vital. Es la base de los filtros electrónicos (para eliminar ruido en señales) y, en electrotecnia de potencia, es el principio fundamental para la corrección del factor de potencia.
Entender el circuito R-C es entender cómo "combatir" los efectos inductivos de las bobinas.
Esquema Eléctrico y Conexión
En esta configuración, conectamos una resistencia (R) en serie con un condensador (C).
– La intensidad (I): la corriente alterna debe atravesar el componente resistivo y el dieléctrico del condensador de forma secuencial.
– La tensión total (V) aplicada: al igual que antes, la intensidad es común, pero la tensión se divide entre los 2 componentes.
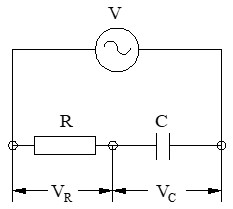
Comportamiento Fasorial
Para visualizar qué ocurre, volvemos a usar la intensidad (I) como nuestro vector de referencia horizontal (0º). Aquí surge la gran diferencia con respecto a las bobinas:
● En la resistencia (VR): la tensión sigue estando en fase con la intensidad. Se dibuja horizontal.
● En la bobina (VL): un condensador se opone a los cambios bruscos de tensión. Esto provoca que el voltaje tarde en subir mientras la corriente ya está circulando. El resultado es que la tensión en el condensador retrasa 90º respecto a la intensidad.
Mientras que en el circuito R-L el vector de de la tensión apuntaba hacia "arriba", en el circuito R-C el vector de tensión capacitiva (VC) apunta hacia "abajo".

Cálculos en el Circuito Serie RC
A efectos de calcular las magnitudes totales (lo que marcaría un polímetro), seguimos utilizando el Teorema de Pitágoras, ya que seguimos teniendo un triángulo rectángulo, solo que invertido.
● Tensión total (V): la suma vectorial de VR (horizontal) y VC (vertical hacia abajo) nos da la tensión de la fuente, obteniéndose el triángulo de tensiones.
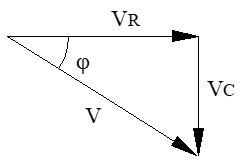
La tensión real de la fuente es la suma vectorial:
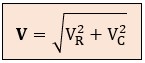
● Impedancia total (Z): del mismo modo que con la bobina, si dividimos los lados del triángulo de tensiones por la intensidad (I), obtenemos el triángulo de impedancias.
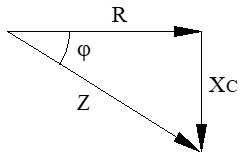
La oposición total al paso de la corriente (Z) se obtiene mediante el triángulo de impedancias.

donde:
R = resistencia en Ohmios (Ω).
XL = reactancia inductiva (2π · f · L) en Ohmios (Ω).
Z = impedancia total en Ohmios (Ω).
El Ángulo de Desfase
El cálculo del ángulo es donde el circuito R-C muestra su verdadera naturaleza "capacitiva". Al aplicar trigonometría en el triángulo de impedancias, debemos tener en cuenta la dirección del vector. Como la reactancia capacitiva (XC) se representa en el eje imaginario negativo:
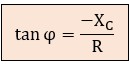
Con lo cual, el desfase φ será:
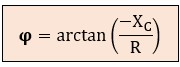
Esto dará como resultado un ángulo φ negativo (entre 0º y -90º).
La interpretación física es que la corriente adelanta. Un ángulo de tensión negativo significa que el vector de tensión total está "por debajo" del de la intensidad.
– En lenguaje técnico, decimos que en un circuito capacitivo, la intensidad adelanta a la tensión.
– Esta propiedad es exactamente la opuesta a la de los motores (circuitos R-L).
¿Por qué es esto útil? Si tenemos una instalación con muchos motores (que retrasan la corriente), podemos conectar condensadores (que adelantan la corriente) para que los efectos se cancelen mutuamente. Esto es lo que se conoce como compensación de energía reactiva.
El Circuito Completo (RLC): Restando Reactancias
Hasta ahora hemos estudiado los componentes por parejas, pero en la realidad, y especialmente en la electrónica y los sistemas de potencia, es común encontrar los 3 elementos (resistencia, inductancia y capacidad) conectados en el mismo lazo.
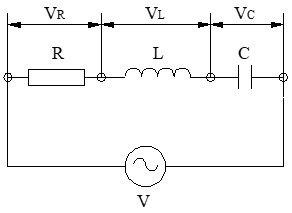
El circuito serie R-L-C es el modelo general. De hecho, los circuitos R-L y R-C que vimos anteriormente no son más que casos particulares de este circuito donde uno de los componentes vale cero.
La Reactancia Inductiva contra la Reactancia Capacitiva
Lo más fascinante de este circuito es la interacción entre la bobina y el condensador. Como vimos en los apartados anteriores:
– La bobina intenta adelantar la tensión 90º (vector hacia arriba, eje y).
– El condensador intenta retrasar la tensión 90º (vector hacia abajo, eje –y).
Físicamente, esto significa que mientras la bobina está absorbiendo energía para crear su campo magnético, el condensador está descargando su campo eléctrico, y viceversa. Son efectos diametralmente opuestos.
En el diagrama fasorial, los vectores de XL y XC forman un ángulo de 180º entre sí. Están en la misma línea vertical, pero tiran en direcciones contrarias. Por tanto, para hallar la reactancia resultante X, no aplicamos Pitágoras entre ellas, sino una resta aritmética directa:
X = XL - XC
El resultado (X) será la reactancia neta que "sobrevive" tras la cancelación mutua.
Los 3 Tipos de Circuitos Posibles RLC
Dependiendo de cuál de las 2 reactancias sea mayor, el circuito adquirirá una "personalidad" distinta. Existen 3 casos posibles:
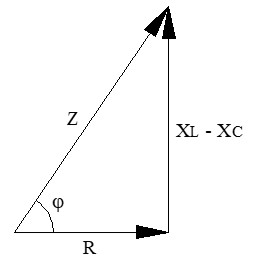
● Predominio inductivo (XL > XC): si la reactancia de la bobina es mayor que la del condensador:
– La resta (XL - XC) es positiva.
– El circuito global se comporta como si fuera un circuito R-L.
– Consecuencia: la corriente total retrasa respecto a la tensión.
– El ángulo de desfase φ es positivo.
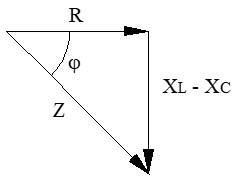
● Predominio capacitivo (XC > XL): si la reactancia del condensador gana la batalla:
– La resta (XL - XC) es negativa.
– El circuito global se comporta como si fuera un circuito R-C.
– Consecuencia: la corriente total adelanta a la tensión.
– El ángulo de desfase φ es negativo.
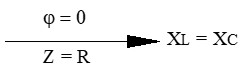
● Resonancia serie (XL = XC): si ambas reactancias son idénticas:
– La resta es cero (X = 0).
– Los efectos reactivos se anulan completamente.
– El circuito se comporta como si solo existiera la resistencia.
– Este fenómeno es tan importante y peligroso que lo detallaremos más adelante (la resonancia).
Cálculos en el Circuito Serie RLC
A efectos de calcular las magnitudes totales, seguimos utilizando el Teorema de Pitágoras, ya que seguimos teniendo un triángulo rectángulo.
● Impedancia total (Z): para calcular la oposición total (Z) en ohmios, la base del triángulo sigue siendo la resistencia (R), pero la altura ahora es la diferencia de reactancias.
Esta es la fórmula para circuitos serie R-L-C:

Al dibujar el triángulo de impedancias:
1º) Dibujamos R en la horizontal.
2º) Dibujamos (XL - XC) en la vertical.
– Si XL > XC, el triángulo apunta hacia arriba (inductivo).
– Si XC > XL, el triángulo apunta hacia abajo (capacitivo).
● Tensión total (V): la suma vectorial de VR (horizontal) y VL - VC (vertical hacia arriba o hacia abajo) nos da la tensión de la fuente, obteniéndose el triángulo de tensiones.
La tensión real de la fuente es la suma vectorial:
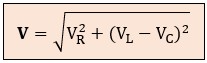
● Ángulo de desfase: al aplicar trigonometría, por ejemplo, en el triángulo de impedancias, el desfase φ que se obtiene será:

Si el ángulo es positivo, el circuito global se comporta como si fuera un circuito R-L. Por el contrario, si el ángulo es negativo, el circuito se comporta como si fuera un circuito R-C.
Potencias en los Receptores Monofásicos en Serie
Hasta ahora hemos hablado de voltios, amperios y ohmios. Sin embargo, en el mundo real, lo que realmente importa para dimensionar una instalación es la potencia.
En corriente continua, la potencia es simple: P = V · I. Pero en corriente alterna, debido a los desfases que introducen las bobinas y condensadores, la historia se complica. La energía no siempre se transforma en trabajo útil; a veces, simplemente "rebota" entre el generador y la carga.
Para entender esto, clasificamos la potencia en 3 tipos que forman un triángulo rectángulo: activa, reactiva y aparente.
Potencia Activa de los Receptores Monofásicos en Serie
Es la potencia útil, la "verdadera". Es la energía eléctrica que realmente se transforma en trabajo físico (calor, luz, movimiento mecánico).
La consume exclusivamente la resistencia (R). Las bobinas y condensadores ideales no consumen potencia activa. Su unidad es el Vatio (W) o Kilovatio (kW). Su fórmula es:

(donde V e I son valores eficaces totales y φ es el ángulo de desfase).
Potencia Reactiva de los Receptores Monofásicos en Serie
Es una potencia "invisible" pero necesaria. No produce trabajo útil (no calienta ni ilumina), pero es imprescindible para crear los campos magnéticos en las bobinas y los campos eléctricos en los condensadores. Esta energía fluctúa: va de la fuente a la carga y vuelve a la fuente 2 veces por cada ciclo de red.
La potencia reactiva es intercambiada por las bobinas y los condensadores. Su unidad es el Voltio-Amperio Reactivo (VAR) o kVAR. Su fórmula general es:

Al igual que con las reactancias, aquí también hay signos opuestos:
– Potencia reactiva inductiva (QL): absorbida por las bobinas (motores, transformadores). Se considera positiva.
– Potencia reactiva capacitiva (QC): generada por los condensadores. Se considera negativa.
La potencia reactiva total (Q) del circuito es la resta aritmética:
Q = QL - QC
Esto explica por qué instalamos baterías de condensadores en las fábricas: generamos QC in situ para anular la QL de los motores, reduciendo la Q que debemos pedir a la red eléctrica.
Potencia Aparente de los Receptores Monofásicos en Serie
Es la potencia total que debe suministrar el generador o transformador para que el circuito funcione. Es la suma vectorial de las 2 anteriores y representa la "carga total" que soportan los cables.
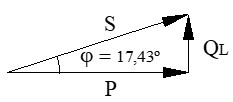
Los transformadores y generadores se dimensionan en kVA (potencia aparente S), no en kW, porque deben soportar tanto la corriente que produce trabajo como la que solo magnetiza. Su unidad es el Voltio-Amperio (VA) o kVA. Su fórmula general es:

Aunque por el triángulo de Pitágoras, también se puede calcular a partir de las potencias activa P y reactiva resultante Q (QL - QC):

En la siguiente figura se muestra un ejemplo del diagrama vectorial de potencias de un circuito serie RLC en el que predomina la potencia reactiva inductiva:
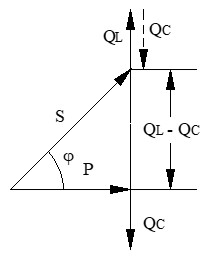
El Factor de Potencia de los Receptores Monofásicos en Serie
El factor de potencia es el indicador más importante de la eficiencia energética de una instalación. Representa qué porcentaje de la potencia total suministrada (S) se está convirtiendo realmente en trabajo útil (P).
La definición matemática del factor de potencia es el coseno del ángulo de desfase.

El rango va de 0 a 1:
– 1 (o 100%): ideal. Toda la energía es útil (Circuito puramente resistivo o en Resonancia).
– Bajo (ej. 0,5): muy ineficiente. La mitad de la corriente que circula por los cables no está produciendo trabajo, pero sí está calentando los conductores y ocupando capacidad del transformador.
Conclusión: Un circuito R-L-C bien diseñado busca que QL y QC sean similares para que se anulen, logrando que S ≈ P y el factor de potencia sea cercano a 1.
Ejercicios Resueltos de Circuitos serie RL, RC y RLC
La teoría de circuitos de corriente alterna se asienta verdaderamente cuando pasamos a los números. A continuación, desarrollamos varios ejemplos.
Ejercicio Resuelto de un Circuito Serie RL
Una bobina de resistencia R = 10 Ω y coeficiente de autoinducción L = 0,01 H, se conecta a una tensión alterna de 230 V, 50 Hz. Calcular:
a) Reactancia de la bobina
b) Impedancia del circuito (dibujar el triángulo de impedancias)
c) Intensidad de la corriente
d) Caídas de tensión en cada componente (dibujar el diagrama vectorial de tensiones e intensidades)
e) Ángulo de desfase entre la tensión y la corriente
f) Factor de potencia
g) Potencia activa, reactiva y aparente (dibujar el triángulo de potencias)
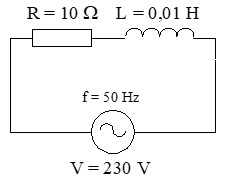
a) Cálculo de la reactancia inductiva (XL): convertimos la inductancia (Henrios) en Ohmios.
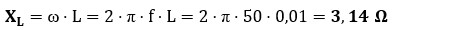
b) Cálculo de la impedancia total (Z): sumamos vectorialmente la resistencia y la reactancia.
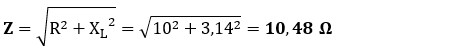
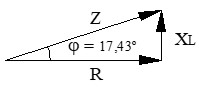
c) Cálculo de la intensidad total (I): aplicamos la Ley de Ohm generalizada.

d) Caídas de tensión parciales:
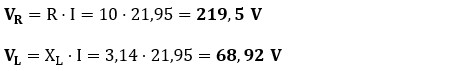
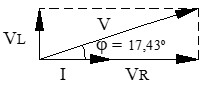
e) Cálculo del ángulo de desfase (φ): determinamos cuánto se retrasa la corriente respecto a la tensión utilizando la tangente del ángulo.
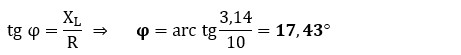
La corriente circula con un retraso de 17,43º respecto a la tensión de la fuente.
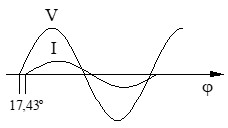
f) Cálculo del Factor de Potencia (FP): es el coseno del ángulo que acabamos de calcular.
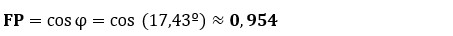
Nota: Es un factor de potencia alto (poco inductivo).
g) Cálculo de potencias (el triángulo de potencias): calculamos las 3 potencias del circuito.
● Potencia aparente (S): la potencia total que suministra la red.
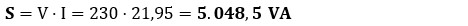
● Potencia activa (P): la que disipa la resistencia en forma de calor.
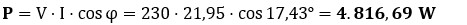
(comprobación alternativa: P = R · I2 = 10 · 21,952 ≈ 4.818 W. La pequeña diferencia se debe al redondeo de decimales).
● Potencia reactiva (QL): la que utiliza la bobina para crear el campo magnético.
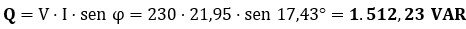
(comprobación alternativa: Q = XL · I2 = 3,14 · 21,952 ≈ 1.512 VAR. La pequeña diferencia se debe al redondeo de decimales).
Ejercicio Resuelto de un Circuito Serie RC
Disponemos de un circuito serie formado por una resistencia R = 300 Ω y un condensador de capacidad C = 16 μF. El conjunto se conecta a una fuente de alimentación de corriente alterna de 230 V y frecuencia f = 50 Hz.
Calcular:
a) Reactancia del condensador
b) Impedancia del circuito (dibujar el triángulo de impedancias)
c) Intensidad de la corriente
d) Desfase entre la tensión y la corriente
e) Tensión en cada componente (dibujar el diagrama vectorial de V e I)
f) Potencia activa, reactiva y aparente (dibujar el triángulo de potencias)
g) Factor de potencia del circuito

a) Reactancia del condensador (XC): primero, debemos convertir la capacidad en Faradios y calcular la oposición que ofrece el condensador al paso de la corriente alterna.
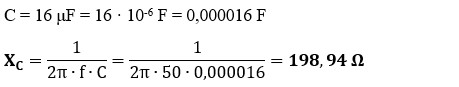
b) Impedancia del circuito (Z): al estar en serie, la oposición total es la suma vectorial de la resistencia (parte real) y la reactancia capacitiva (parte imaginaria).
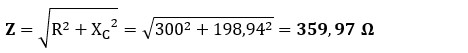
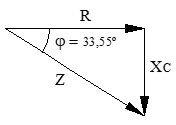
c) Intensidad de corriente (I): aplicamos la Ley de Ohm para corriente alterna usando la impedancia total calculada.

d) Desfase entre la tensión y la corriente (φ): calculamos el ángulo mediante la tangente. En circuitos capacitivos, el ángulo es negativo porque la intensidad adelanta a la tensión.
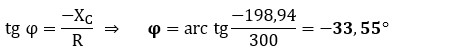
La corriente está adelantada 33,55º respecto a la tensión de alimentación.
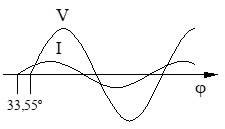
e) Tensión en cada componente (VR y VC): calculamos las caídas de tensión parciales multiplicando la intensidad común por la oposición de cada componente.
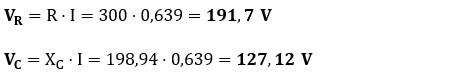
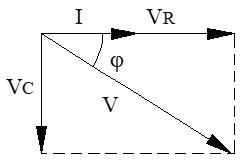
f) Potencia activa, reactiva y aparente (P, Q y S):
● Potencia aparente (S): (total suministrada)
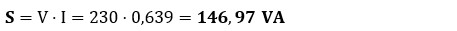
● Potencia activa (P): (Trabajo útil / Calor)
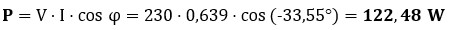
● Potencia reactiva (QC): (Energía de campo eléctrico)
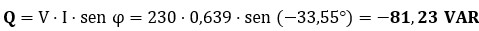
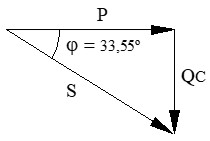
g) Factor de Potencia (FP):
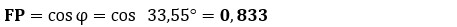
Ejercicio Resuelto de un Circuito Serie RLC
Se conecta un circuito serie compuesto por una resistencia R = 12 Ω, una bobina de inductancia L = 42 mH y un condensador de capacidad C = 127 μF. El sistema se alimenta con una fuente alterna monofásica de 230 V y una frecuencia de 50 Hz. Obtener:
a) Reactancias de bobina y condensador
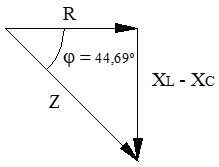
b) Impedancia del circuito (dibujar el triángulo de impedancias)
c) Corriente del circuito
d) Caídas de tensión en cada componente (dibujar el diagrama vectorial)
e) Desfase entre la tensión y la corriente
f) Potencia activa, reactiva y aparente (dibujar el triángulo de potencias)
g) Factor de potencia
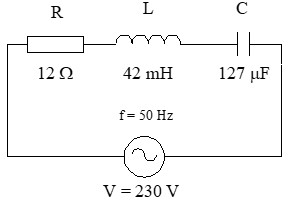
a) Reactancias de bobina (XL) y condensador (XC): primero convertimos los efectos inductivos y capacitivos a Ohmios (Ω) para poder operar con ellos.
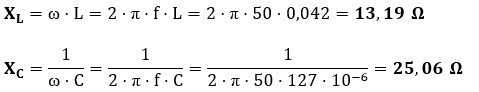
Análisis preliminar: como XC > XL (25,06 > 13,19), el circuito tendrá un comportamiento global capacitivo.
b) Impedancia del circuito (Z): calculamos la oposición total. Primero hallamos la reactancia neta (X) restando los valores anteriores (XL - XC):
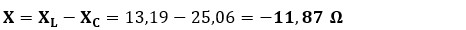
Ahora aplicamos Pitágoras con la resistencia:
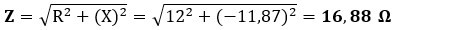
c) Corriente del circuito (I): al ser un circuito serie, la corriente es única para todos los componentes.

d) Caídas de tensión en cada componente: aplicamos la Ley de Ohm individualmente:

La corriente (I) es la referencia horizontal. VR está sobre ella. VL va 90º hacia arriba y VC va 90º hacia abajo (siendo este vector más largo que el de la bobina).
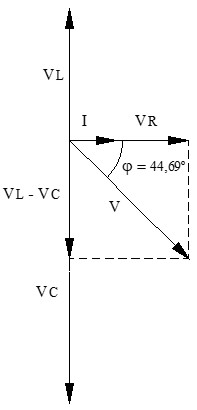
e) Desfase entre la tensión y la corriente (φ):
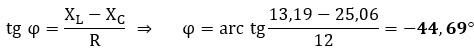
El ángulo es negativo, lo que confirma que la corriente adelanta 44,69º respecto a la tensión total.
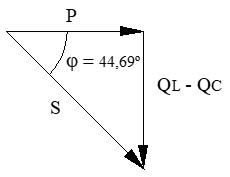
f) Potencia activa, reactiva y aparente:

El signo negativo indica carácter capacitivo, es decir, el circuito genera reactiva hacia la red.
g) Factor de Potencia (FP):
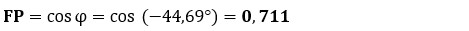
La Resonancia Serie: Cuando XL anula a XC
Dentro del estudio del circuito serie R-L-C, existe un caso singular que merece una atención especial por sus implicaciones prácticas y riesgosos efectos físicos: la resonancia eléctrica en serie.
Este fenómeno no ocurre al azar; sucede en un momento muy preciso donde las propiedades de la bobina y el condensador se equilibran perfectamente, anulando sus efectos reactivos entre sí.
La Condición de Resonancia de los Receptores en Serie
La resonancia en serie se produce exclusivamente cuando la reactancia inductiva es igual a la reactancia capacitiva:
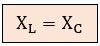
Dado que XL aumenta con la frecuencia y XC disminuye con ella, solo existe una única frecuencia (fr) para cada combinación de bobina y condensador donde estos valores se cruzan y son idénticos.
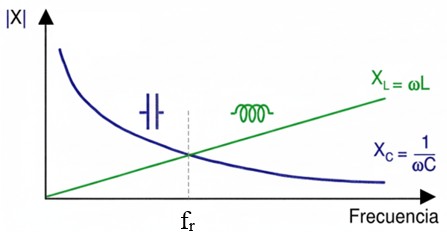
Impedancia Mínima y Corriente Máxima de los Receptores en Serie
Cuando se cumple la condición anterior, la fórmula de la impedancia total sufre una transformación drástica:
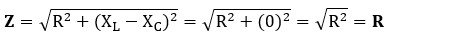
Esto desencadena 2 consecuencias inmediatas:
● Impedancia mínima: el circuito se comporta como si fuera puramente resistivo. Toda la oposición reactiva desaparece. La impedancia (Z) cae a su valor más bajo posible (solo el valor de R).
● Intensidad máxima: según la Ley de Ohm (I = V/Z), si la impedancia es mínima, la intensidad se dispara hasta su valor máximo posible.
Advertencia: Si la resistencia interna del circuito (R) es muy pequeña, la corriente en resonancia puede ser destructiva, similar a un cortocircuito.
Frecuencia de Resonancia de los Receptores en Serie
Podemos determinar a qué frecuencia ocurrirá este fenómeno igualando las fórmulas de las reactancias y despejando la frecuencia (f):

Despejando finalmente f, obtenemos la fórmula de Thomson para la frecuencia de resonancia (fr):
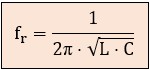
Peligro de Sobretensiones en los Receptores en Serie
Este es el punto más crítico para la seguridad. Aunque la tensión total de la fuente sea baja (ej. 230 V), dentro del circuito pueden estar ocurriendo fenómenos violentos.
Como la intensidad (I) es muy alta, al multiplicarla por las reactancias individuales (VL = XL · I y VC = XC · I), podemos obtener caídas de tensión en la bobina y el condensador que superan ampliamente la tensión de alimentación. Podríamos tener una fuente de 230 V, pero medir 1000 V en los bornes del condensador.
Esto ocurre porque VL y VC son iguales y opuestos, por lo que se anulan mutuamente de cara a la fuente, pero están presentes físicamente en los componentes, pudiendo perforar el aislamiento del condensador o quemar la bobina.
Aplicaciones de la Resonancia Serie
Aunque la resonancia en serie puede ser destructiva si ocurre accidentalmente en una red de distribución, en el mundo de la electrónica y las telecomunicaciones es una herramienta de precisión inestimable. Su propiedad fundamental, la de ofrecer una impedancia mínima (Z ≈ 0) a una frecuencia específica, se aprovecha para "limpiar" señales.
El circuito serie L-C se utiliza habitualmente para eliminar una frecuencia molesta o parásita dentro de una señal compleja compuesta por multitud de frecuencias.
La configuración es la siguiente: se conecta el circuito oscilante serie en derivación (paralelo) entre la línea de señal y tierra.
– Para la frecuencia de resonancia (fr): el circuito L-C presenta una impedancia casi nula. Actúa como un "agujero" o cortocircuito selectivo, desviando toda la energía de esa frecuencia específica hacia tierra. La señal desaparece de la salida.
– Para el resto de frecuencias: el circuito presenta una alta impedancia (ya sea inductiva o capacitiva), por lo que no afecta al paso de la señal, que continúa su camino inalterada.
Por ejemplo, esta configuración se usa en equipos de audio o instrumentación para eliminar el "zumbido" de 50 Hz o 60 Hz inducido por la red eléctrica, sin afectar a la música o a los datos que viajan a frecuencias superiores.
También te puede interesar:

Condensador Eléctrico (Capacitor): Qué es, Tipos, Código y Fórmulas
Bobina o Inductor Eléctrico: Qué es, Símbolo y Funcionamiento (Ley de Lenz)
Generación de Corriente Alterna: El Alternador y la Inducción Electromagnética
Parámetros de la Onda Senoidal (CA): Frecuencia, Periodo y Valor Eficaz (RMS)
Receptores en Corriente Alterna: Circuitos R, L y C (Resistivo, Inductivo y Capacitivo)

Receptores en Paralelo (RLC): Cálculo de Corrientes y Potencias
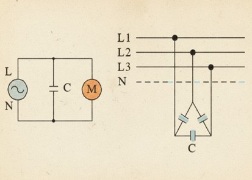
Factor de Potencia (cos φ) y Energía Reactiva: Qué es y Cómo Corregirlo
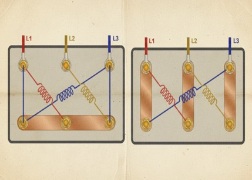
Conexión Estrella y Triángulo: Diferencias, Esquemas y Voltajes (230/400V)