Conexión Estrella y Triángulo: Diferencias, Esquemas y Voltajes (230/400V)
¿Alguna vez has abierto la caja de bornas de un motor y has visto 6 tornillos y unas chapitas metálicas? Ahí es donde se decide la conexión Estrella o Triángulo. Esta configuración determina si las bobinas de la máquina reciben 230V o 400V.
Elegir correctamente entre Estrella (Y) y Triángulo (Δ) es vital: una mala elección puede hacer que el motor tenga poca fuerza o, peor aún, que se queme instantáneamente.
En esta guía te explicamos la relación matemática (√3), cómo colocar las chapas en la placa de bornas y cuándo usar el famoso Arranque Estrella-Triángulo.
Los sistemas trifásicos de corriente alterna representan uno de los desarrollos más significativos en la historia de la ingeniería eléctrica.
La implementación práctica de estos sistemas demostró rápidamente ventajas económicas y técnicas tan importantes sobre los sistemas monofásicos y bifásicos existentes que, para finales del siglo XIX, ya se habían establecido como el estándar para la generación, transmisión y distribución de energía eléctrica a nivel industrial.
Contenidos
- Qué es la Corriente Trifásica
- Configuración de las Bobinas del Generador Trifásico
- Valores Compuestos (de Línea) y Simples (de Fase)
- Relaciones en la Conexión Estrella (Y)
- Relaciones en la Conexión Triángulo (Δ)
- Cargas Trifásicas Equilibradas
- El Papel Vital del Neutro (Solo en Estrella)
- Arranque Estrella-Triángulo: Reducir el Pico de Corriente
Qué es la Corriente Trifásica
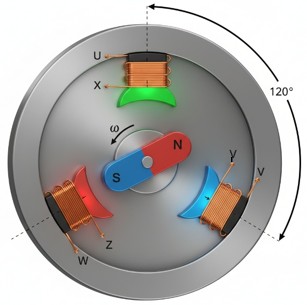
Un sistema trifásico es aquel constituido por 3 corrientes alternas monofásicas de igual frecuencia y amplitud (valor eficaz), que presentan una diferencia de fase entre ellas de 120º (o 2π/3 radianes) eléctricos.
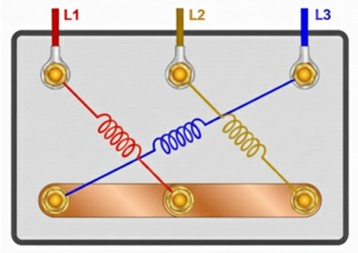
Si imaginamos un generador con 3 bobinas independientes dispuestas físicamente a 120º una de la otra. Al girar el rotor magnético, se inducen 3 tensiones que alcanzan sus valores máximos en momentos sucesivos y ordenados.
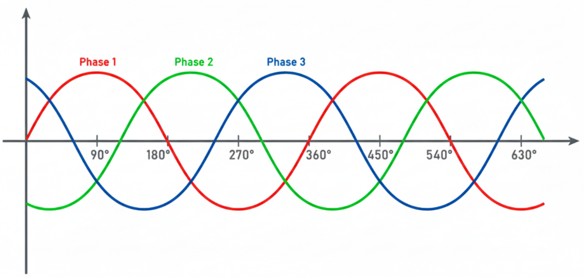
Matemáticamente, si tomamos la tensión de una de las bobinas como referencia, por ejemplo la de la fase 1, las tensiones instantáneas se definen como:
- Fase 1 ⇒ v1(t) = Vmáx · sen (ω · t)
- Fase 2 ⇒ v2(t) = Vmáx · sen (ω · t – 120º)
- Fase 3 ⇒ v3(t) = Vmáx · sen (ω · t – 240º)
Esta simetría es lo que denominamos un sistema equilibrado.
Tal y como se muestra en la siguiente figura, el sistema trifásico genera 3 ondas de CA idénticas en magnitud y frecuencia, pero que alcanzan sus valores pico en momentos diferentes y secuenciales.
Necesidad de Interconectar las 3 Bobinas
Si tratáramos cada una de estas 3 fases (3 bobinas) como circuitos independientes, necesitaríamos 2 cables para cada una (ida y retorno), sumando un total de 6 conductores. Esto sería económica y técnicamente inviable para el transporte de energía a largas distancias.
La solución es la interconexión de las bobinas entre sí. Al unir los terminales de una forma específica, podemos reducir el número de conductores necesarios de 6 a solo 3 o 4 cables (las 3 fases L1, L2, L3 y opcionalmente el Neutro N).
Existen 2 formas topológicas fundamentales de realizar esta interconexión, en estrella o en triángulo. La elección de una u otra cambiará radicalmente el comportamiento de la tensión y la corriente en el circuito.
Topologías en Estrella y Triángulo
Estas configuraciones definen cómo se unen los principios y finales de las bobinas (o de las cargas):
● Configuración en estrella (símbolo Y): en esta conexión, unimos los terminales finales de las tres bobinas (o cargas) en un punto común denominado centro de estrella o punto neutro.
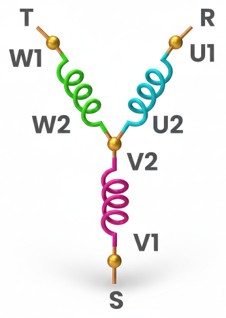
– Característica visual: se asemeja a la letra "Y".
– Conexión: los extremos libres se conectan a las líneas de alimentación (L1, L2, L3).
– El neutro: desde el punto común central se puede (o no) sacar un cuarto conductor: el Neutro. Esto es vital porque permite tener 2 niveles de tensión disponibles (ej. 400 V entre fases y 230 V entre fase y neutro).
● Configuración en triángulo (símbolo Δ): aquí no existe un punto común. El final de la primera bobina se conecta al principio de la segunda, el final de la segunda al principio de la tercera, y el final de la tercera cierra el circuito conectándose al principio de la primera.
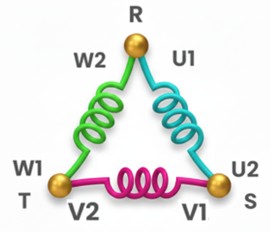
– Característica visual: forman un bucle cerrado, similar a la letra griega Delta (Δ).
– Conexión: las líneas de alimentación se conectan en los vértices de unión entre bobinas.
– Sin neutro: en esta configuración no existe neutro. Solo tenemos acceso a un nivel de tensión (la tensión de línea), y la corriente debe circular obligatoriamente a través de las fases.
Configuración de las Bobinas del Generador Trifásico
En cualquier circuito eléctrico, es fundamental distinguir entre la fuente (quien suministra la energía) y la carga (quien la consume). Aunque las conexiones estrella y triángulo se aplican a ambos lados, su comportamiento y utilidad son diferentes dependiendo de dónde estemos mirando.
En este apartado nos centraremos en el origen de la energía: el generador (o, en la práctica habitual de distribución, el secundario del transformador que alimenta la red). La forma en que conectemos las bobinas internas del generador determinará qué tensiones tendremos disponibles para su uso.
Generador Trifásico con Conexión en Estrella (Y)
Es la configuración más utilizada en la generación y distribución de baja tensión a nivel mundial.
En un generador conectado en estrella, los 3 finales de las bobinas X, Y, Z (o también U2, V2, W2) se unen física y eléctricamente en un punto común.
Los 3 principios de las bobinas U, V, W (o también U1, V1, W1) quedan libres y se conectan a los conductores de salida, que son las Fases o Líneas (L1, L2, L3).
Presencia de Neutro: el punto común donde se unen las 3 bobinas se denomina centro de estrella o punto neutro. La característica de esta conexión es que nos permite sacar un cuarto conductor desde este punto: el Neutro (N).
La presencia del neutro dota al sistema de una versatilidad única, ofreciendo 2 niveles de tensión simultáneos:
● Tensión de línea o compuesta (VL): medida entre 2 fases cualquiera (ej. L1 y L2). En Europa, estándar de 400 V.
● Tensión de fase o simple (VF): medida entre una fase y el neutro (ej. L1 y N). En Europa, estándar de 230 V.
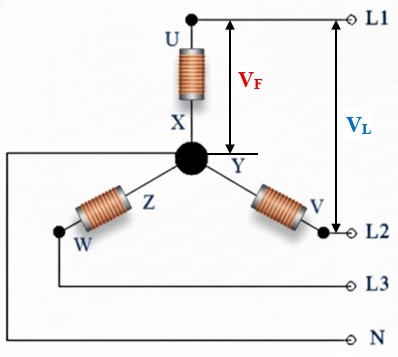
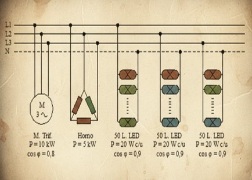
La conexión en estrella permite alimentar cargas trifásicas de potencia (como motores a 400 V) y, al mismo tiempo, cargas monofásicas domésticas (alumbrado y tomas de corriente a 230 V) conectándolas entre una fase y el neutro.
Además, conectar el punto neutro a tierra en el origen garantiza la estabilidad de los potenciales respecto al suelo, fundamental para la seguridad eléctrica.
Generador Trifásico con Conexión en Triángulo (Δ)
Esta configuración es menos común para alimentar redes de distribución final de baja tensión, pero es muy habitual en redes de media tensión o en transformadores de aislamiento.
En un generador conectado en triángulo, las bobinas se conectan en serie formando un bucle cerrado o malla, de forma que, el final de la bobina 1 se conecta al principio de la bobina 2, el final de la bobina 2 se conecta al principio de la bobina 3 y el final de la bobina 3 cierra el circuito conectándose al principio de la bobina 1. De los 3 vértices de unión salen los conductores de línea (L1, L2, L3).
Ausencia de Neutro: la diferencia más evidente es que no existe un punto común. Por tanto, en un sistema en triángulo puro (3 hilos), no podemos disponer de conductor neutro.
Esto implica que solo existe un nivel de tensión disponible: la tensión de línea (VL). La tensión que genera cada bobina es idéntica a la tensión que se entrega a la red (VF = VL).
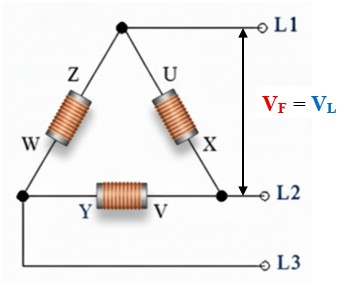
La conexión en triángulo conlleva riesgos técnicos específicos:
– Corrientes internas: si las fuerzas electromotrices (f.e.m.) generadas en las 3 bobinas no son perfectamente senoidales o no están perfectamente equilibradas en amplitud y fase, la suma vectorial de las tensiones dentro del bucle cerrado no será cero.
– Consecuencia: esto provoca que aparezca una corriente que circula permanentemente dentro del triángulo (corriente de circulación), incluso sin tener ninguna carga conectada. Esta corriente inútil genera calor, pérdidas de energía y puede sobrecalentar los devanados.
– Armónicos: especialmente problemáticos son los terceros armónicos, que tienden a circular dentro de la conexión en triángulo, quedando "atrapados" (lo cual a veces se usa como ventaja en transformadores para no enviarlos a la red, pero calienta la máquina).
Valores Compuestos (de Línea) y Simples (de Fase)
Para dimensionar cables, elegir protecciones o calcular potencias, debemos dominar la relación entre lo que medimos en la red (Línea) y lo que ocurre dentro de la máquina (Fase). Es fundamental distinguir entre los valores "externos" (de línea) y los "internos" del circuito (de fase).
● Tensión de Línea (VL): es la tensión compuesta. Se mide entre 2 fases diferentes (L1-L2, L2-L3, etc.). Es el voltaje que nos da la compañía eléctrica o la red de distribución. Ejemplo estándar: 400 V en trifásica industrial europea. En un motor se mediría en los conductores externos de alimentación.
● Tensión de Fase (VF): es la tensión simple o tensión sobre la carga. Se define como la tensión que soporta cada una de las bobinas o impedancias individualmente en sus bornes. En un motor se mediría entre los extremos de una de las 3 bobinas internas.
● Corriente de Línea (IL): es la intensidad que circula por cada cable de alimentación del sistema (L1, L2 o L3). En un motor es la que mediríamos con una pinza amperimétrica abrazando uno de los conductores externos de alimentación.
● Corriente de Fase (IF): es la intensidad que circula internamente por cada rama (impedancia o bobina) del receptor. Es la que mediríamos con una pinza amperimétrica abrazando uno de los conductores de una de sus 3 bobinas internas.
Relaciones en la Conexión Estrella (Y)
Si ahora nos centramos en las cargas o receptores, en la conexión estrella, las cargas (impedancias) se conectan entre una fase y un punto común (neutro).
Cómo Conectar un Motor en Estrella (Y)
En el caso de querer alimentar un motor trifásico en estrella, se unen los 3 finales (o los 3 principios) en un punto común (neutro de la estrella).
Esto se logra típicamente en su placa de bornas, poniendo chapas horizontales que unen los finales (o principios) de las bobinas. La alimentación (L1, L2, L3) se conecta a los principios (o finales).
Corrientes en Estrella (Y)
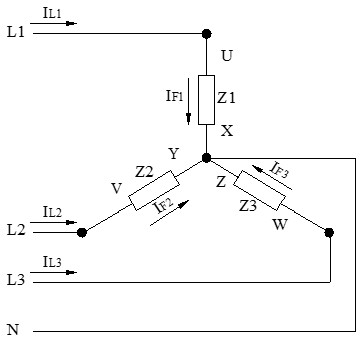
Observando el siguiente esquema, vemos que el conductor de línea se conecta directamente al principio de la bobina o impedancia. No hay nudos ni derivaciones previas. Por lo tanto, toda la corriente que viene por la línea debe pasar obligatoriamente por la fase.
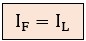
En consecuencia, en estrella, la corriente de línea y de fase son idénticas.
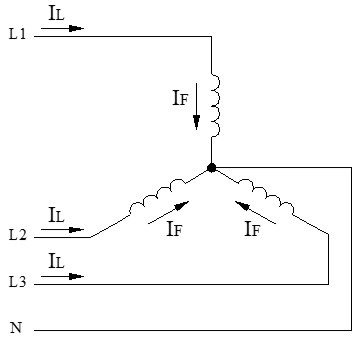
Voltajes en Estrella (Y)
Aquí la situación cambia. La tensión de línea (VL) se aplica entre 2 terminales (ej. L1 y L2). Sin embargo, entre L1 y L2 tenemos 2 bobinas o impedancias en serie conectadas al punto neutro.
Mediante suma vectorial (no aritmética), se demuestra que la tensión de línea es mayor que la de fase. El factor de relación es la raíz cuadrada de 3 (≈1,732), siendo VL = √3 · VF. De aquí despejamos la tensión que soporta la carga:

Por ejemplo, si tenemos una red de 400 V (VL), cada bobina del motor en estrella recibirá 400 / 1,73 ≈ 230 V.
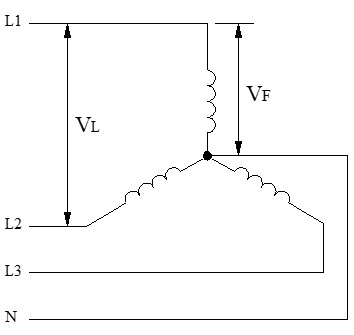
Diagrama Fasorial
Al dibujar los vectores, vemos que la tensión de línea no está en fase con la tensión de fase. Existe un adelanto de 30° de la tensión de línea respecto a la tensión de fase correspondiente.
Por ejemplo, la tensión de línea VL1-L2 tiene un adelanto de 30° respecto de la tensión de fase VL1-N.
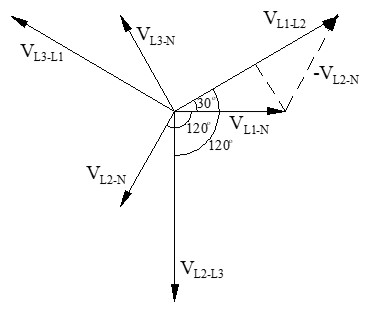
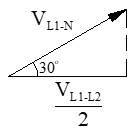
Aplicando trigonometría al triángulo rectángulo que se obtiene, podemos hallar la relación que existe entre tensión de fase (simple) y tensión de línea (compuesta) en un generador trifásico con conexión en estrella:
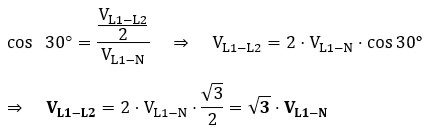
Relaciones en la Conexión Triángulo (Δ)
En esta conexión, las cargas (impedancias) se conectan directamente entre 2 fases. Esto invierte la lógica anterior.
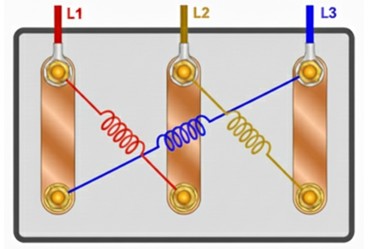
Cómo Conectar un Motor en Triángulo (Δ)
En el caso de querer alimentar un motor trifásico en triángulo, se unen el final de una bobina con el principio de la siguiente (o principio de una bobina con final de la siguiente).
Esto se logra típicamente en su placa de bornas, poniendo 3 chapas verticales que unen pares o parejas específicas (finales y principios de diferentes bobinas). La alimentación (L1, L2, L3) se conecta a esos pares.
Voltajes en Triángulo (Δ)
Tal y como se observa en el siguiente esquema, al estar cada impedancia conectada directamente a los conductores de línea (ej. entre L1 y L2), la tensión que "ve" la carga es exactamente la misma que hay en la red.
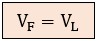
Por tanto, en triángulo, la bobina recibe toda la tensión de la red (400 V).
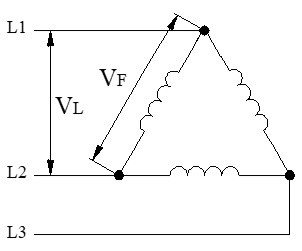
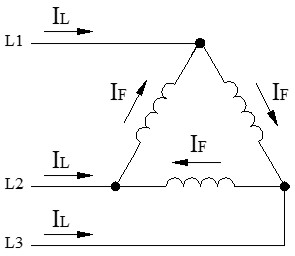
Corrientes en Triángulo (Δ)
Aquí la corriente de línea (IL) llega a un vértice del triángulo (un nodo) y se tiene que dividir hacia 2 ramas diferentes.
Aplicando la Ley de Kirchhoff vectorial, la corriente de línea es la suma vectorial de las 2 corrientes de fase que concurren en el nodo. Al igual que pasaba con las tensiones en la estrella, aquí aparece el factor √3 (≈1,732), siendo IL = √3 · IF. De aquí deducimos la corriente que soporta cada bobina:
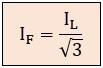
Por ejemplo, si medimos 100 A en el cable de alimentación, por dentro del motor (por cada bobina) solo están circulando 57,7 A.
Cargas Trifásicas Equilibradas
Esta parte conecta la teoría con la realidad de los equipos que instalamos (motores, baterías de condensadores, resistencias de calentamiento, etc.).
El objetivo final de cualquier instalación eléctrica es alimentar un receptor o carga. En trifásica, estos receptores pueden ser pasivos (como un horno de resistencias) o inductivos (como un motor asíncrono).
Para analizar su comportamiento, partimos de un escenario ideal: la carga equilibrada. Esto ocurre cuando conectamos 3 impedancias idénticas a la red trifásica.
Se comprobará que calcular la potencia en un sistema trifásico equilibrado es idéntica, independientemente de que la carga esté conectada en estrella o en triángulo.
Carga Equilibrada en Estrella (Y)
Decimos que una carga es equilibrada en estrella cuando las 3 impedancias conectadas (Z1, Z2, Z3) son idénticas en magnitud y en ángulo de fase.
Corriente Nula por el Neutro en Estrella
Como hemos dicho, la tensión de línea VL (entre fase y fase) es mayor que la tensión de fase VF (entre bornes de cada impedancia), siendo VL = √3 · VF. Por otro lado, la corriente de línea IL (la que pasa por la línea de alimentación) es igual a la corriente de fase IF (la que pasa por la impedancia), siendo IF = IL.
En una conexión estrella, las corrientes de las 3 fases confluyen en el punto central o centro de estrella.
Según la primera Ley de Kirchhoff, la corriente que retorna por el neutro (IN) debe ser la suma vectorial de las corrientes que entran:
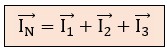
En un sistema equilibrado, estas 3 corrientes tienen el mismo valor numérico (Amperios) pero están desfasadas 120º exactos una de la otra. Si realizamos la suma vectorial de estos tres fasores, el resultado es sorprendente: se anulan entre sí.

Dado que la resultante de corriente es cero, el conductor neutro se vuelve innecesario desde el punto de vista funcional.
Por esta razón, la mayoría de los receptores trifásicos equilibrados (como los motores) solo tienen 3 bornes de conexión (más la tierra de protección) y no requieren cable neutro para funcionar. Un amperímetro en el neutro de una carga perfectamente equilibrada, marcaría 0 A.
Potencias en Estrella
Para calcular la potencia trifásica P (potencia total) en una carga equilibrada conectada en estrella, se suman las potencias de cada fase:

Cada impedancia soporta la tensión de fase (VF) y es recorrida por la corriente de fase (IF) y, como la potencia de cada fase es P = V · I · cos φ:
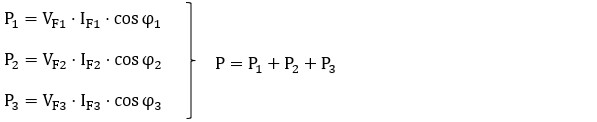
Además, se cumple que: VL = √3 · VF, IF = IL y, por ser un sistema equilibrado, las tensiones, corrientes y ángulos son iguales en todas las fases. Sustituyendo y operando, la potencia total en función de los valores de línea resulta:
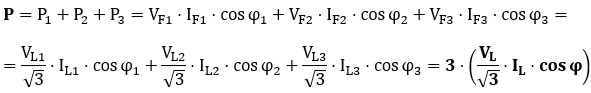
Y multiplicando y dividiendo por √3 queda:

Mediante el mismo procedimiento se demuestra que:

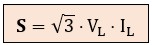
Carga Equilibrada en Triángulo (Δ)
Igualmente decimos que una carga es equilibrada en triángulo cuando las 3 impedancias conectadas (Z1, Z2, Z3) son idénticas en magnitud y en ángulo de fase.
Ausencia del Punto Neutro en Triángulo
Como hemos dicho, la tensión de línea VL (entre fase y fase) es igual que la tensión de fase VF (entre bornes de cada impedancia), siendo VL = VF. Por otro lado, la corriente de línea IL (la que pasa por la línea de alimentación) es mayor a la corriente de fase IF (la que pasa por la impedancia), siendo IL = √3 · IF.
En la conexión en triángulo las 3 corrientes de línea o compuestas IL salen de la fuente de alimentación y pasan por las fases L1, L2 y L3, siendo estas corrientes mayores que las corrientes de fase o simples por cada impedancia, de forma que IL = √3 · IF.
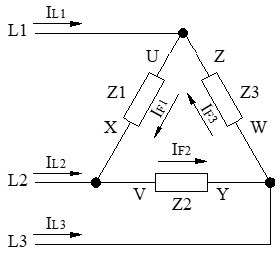
Potencias en Triángulo
Para el cálculo de la potencia trifásica P (potencia total) en una carga equilibrada conectada en estrella, se suman las potencias de cada fase:

Cada impedancia soporta la tensión de línea (VL) que es la misma que la de fase (VF) y es recorrida por la corriente de fase (IF). Como la potencia de cada fase es P = V · I · cos φ:
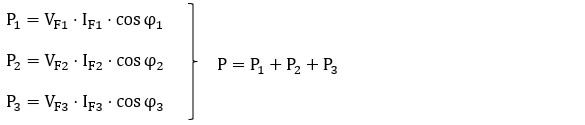
Además, se cumple que: IL = √3 · IF, VF = VL y, por ser un sistema equilibrado, las tensiones, corrientes y ángulos son iguales en todas las fases. Sustituyendo y operando, la potencia total en función de los valores de línea resulta:
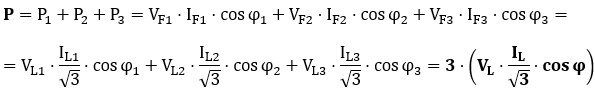
Y multiplicando y dividiendo por √3 queda:

Mediante el mismo procedimiento se demuestra que:

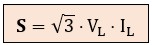
Comparación de Potencias en Estrella y en Triángulo
En el análisis de sistemas trifásicos equilibrados, una cuestión fundamental que surge frecuentemente es comprender cómo se comporta una misma impedancia cuando se conecta en estrella (Y) o triángulo (Δ).
● Proporción entre las corrientes de fase: la corriente de fase en una impedancia se calcula con la Ley de Ohm.
– En estrella (Y):

– En triángulo (Δ):
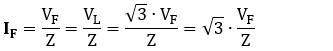
La proporción entre las corriente de fase IF, en triángulo (Δ) y en estrella (Y), es de √3.
● Proporción entre las corrientes de línea: la corriente de línea se relaciona con la corriente de fase de la siguiente manera:
– En estrella (Y):

– En triángulo (Δ):

Para obtener la proporción entre las corrientes de línea, comparamos las corrientes de línea en ambas configuraciones:
– En estrella (Y):

– En triángulo (Δ):
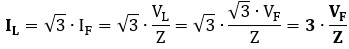
(teniendo en cuenta que VL = √3 · VF)
La proporción entre las corrientes de línea IL, en triángulo (Δ) y en estrella (Y), es de 3.
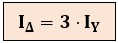
Puesto que la fórmula de potencia trifásica es la misma tanto para estrella como para triángulo, la misma proporción existirá entre las potencias, siendo la potencia en triángulo (Δ) el triple de la potencia en estrella (Y) para las mismas impedancias:
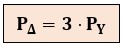
¿Por qué ocurre esto? Al cambiar a triángulo, aumentamos la tensión que recibe la impedancia de carga por √3. Como la potencia monofásica de una impedancia depende del cuadrado de la tensión (P = V2 / Z), el aumento de potencia es (√3)2 = 3.
Esto explica por qué un motor arranca con "menos fuerza" en estrella. Al conectarlo en estrella, reducimos su tensión y, por tanto, su potencia y par se reducen a la tercera parte, lo que suaviza el pico de corriente de arranque. Una vez el motor toma velocidad, pasamos a triángulo para obtener el 100% de su potencia nominal.
El Papel Vital del Neutro (Solo en Estrella)
Las fórmulas globales de la potencia trifásica P, Q y S, en función de √3 no son válidas directamente cuando el sistema está desequilibrado.
¿Por qué? Porque esa fórmula asume que IL es igual en las 3 fases. Por ejemplo, Si tenemos 10 A en la fase L1, 50 A en la L2 y 20 A en la L3, ¿qué valor pondríamos en la fórmula? No podemos usar un promedio.
Si se parte de cargas no idénticas (cargas desequilibradas) el sistema pierde su simetría. Para calcular las potencias y corrientes, debemos abandonar el enfoque "global" y utilizar el enfoque "fase por fase".
Debemos tratar el sistema como 3 circuitos monofásicos independientes que comparten un punto común (el Neutro).
Cálculo con Cargas Trifásicas Desequilibradas
El procedimiento de cálculo consiste en calcular cada fase por separado. Debemos calcular la potencia activa (P), reactiva (Q) y aparente (S) de la Fase 1, luego de la Fase 2 y luego de la Fase 3, usando los datos específicos de cada una (su propia corriente y su propio factor de potencia).
La potencia activa total P se obtendría de esta forma:

Y de forma análoga, la potencia reactiva total Q se obtendría así:
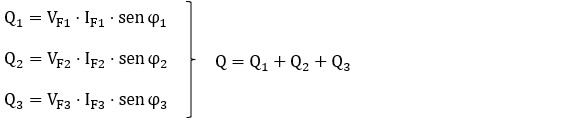
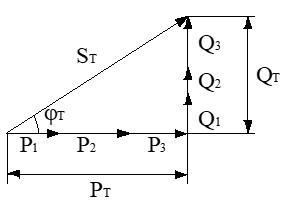
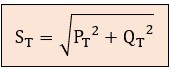
⚠️ ¡Cuidado!: para calcular la potencia aparente total S no se pueden sumar las potencias aparentes (S ≠ S1 + S2 + S3) porque los ángulos son distintos. Debemos usar el triángulo de potencias total (Pitágoras):
Cuando el sistema está desequilibrado, por el neutro sí circula corriente. Para calcularla, no basta con sumar los amperios (suma escalar), hay que hacer una suma vectorial, teniendo en cuenta que cada corriente tiene en una dirección diferente.
Como ya vimos, la corriente que retorna por el neutro (IN) debe ser la suma vectorial de las corrientes que entran:
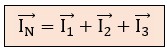
Para resolver esto, se pueden descomponer las corrientes en coordenadas rectangulares (ejes X e Y), o bien, mediante números complejos.
Función del Neutro en Sistemas Trifásicos Desequilibrados
En el mundo real las cargas son diferentes entre sí. Al diseñar instalaciones trifásicas se intenta repartir las cargas monofásicas entre las 3 fases de forma que el equilibrado de cargas sea lo más óptimo posible.
Aquí es donde el conductor neutro pasa de ser un "accesorio opcional" a convertirse en indispensable para la garantía de seguridad en la instalación eléctrica cuando hay desequilibrios.
Por ejemplo, imaginemos un edificio de viviendas alimentado por una derivación individual trifásica. El piso 1ºA está conectado a la Fase 1, el 1ºB a la Fase 2 y el 1ºC a la Fase 3.
- En el 1ºA: tienen encendido el aire acondicionado y el horno (mucha carga, baja impedancia).
- En el 1ºB: no hay nadie, solo un router wifi conectado (poca carga, alta impedancia).
- En el 1ºC: tienen luces LED (carga media).
Esto es un sistema desequilibrado. Las impedancias de cada rama son diferentes (Z1 ≠ Z2 ≠ Z3).
Al ser las impedancias distintas, las corrientes que retornan al centro de estrella no se anulan entre sí vectorialmente (I1 + I2 + I3 ≠ 0). Existe una corriente resultante que debe retornar por el cable neutro (IN).
Gracias a que el centro de la estrella está conectado físicamente al neutro del transformador (que está a potencial 0 V), se fuerza a que el punto común de las cargas se mantenga a 0 V. Esto garantiza que, independientemente de lo que consuma cada vecino, todos reciban la misma tensión de fase (VF = 230 V).
Corte Accidental del Neutro en Trifásica
Ocurre cuando, en un sistema trifásico con cargas desequilibradas, se rompe, se desconecta o se corroe el conductor neutro aguas arriba (antes de llegar a las cargas).
Si el conductor neutro distribuido desde el transformador está bien conectado, el punto común de nuestra instalación está anclado a 0 V (potencial de tierra). Cada fase tendrá la misma tensión (U1, U2, U3) respecto al neutro de 230 V.
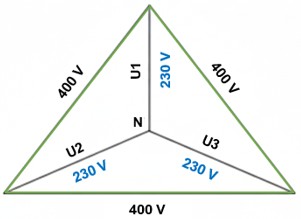
Al perder la conexión con el neutro del transformador, el punto común deja de estar anclado a 0 V. Queda el "neutro flotante". El nuevo potencial del punto central dependerá de la relación entre las impedancias de los vecinos.
Vectorialmente, el punto central (N') se desplaza desde el centro geométrico hacia la fase que tiene más carga (menor impedancia). Ahora, cada una de las fases tendrá diferente tensión (U1’, U2’, U3’) respecto al neutro.
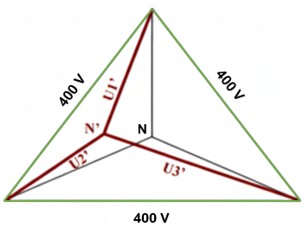
Esto rompe la simetría de las tensiones con consecuencias desastrosas:
● Fases con MUCHA carga (subtensión): al tener baja resistencia (muchos aparatos conectados), la tensión cae en sus bornes. Los vecinos con el horno encendido verán que la luz se atenúa o parpadea. Recibirán quizás 150 V o 100 V.
● Fases con POCA carga (sobretensión): al tener alta resistencia (pocos aparatos), la tensión aumenta en ellos. El vecino que solo tenía el router conectado (carga ligera) sufrirá una subida de tensión brutal. Su enchufe dejará de tener 230 V y se acercará peligrosamente a la tensión de línea (400 V).
Por esta razón las protecciones (magnetotérmicos) de corte omnipolar deben cortar el neutro al mismo tiempo o después que las fases, y conectar al mismo tiempo o antes, nunca al revés.
La solución para mitigar el riesgo de sobretensión por corte del conductor neutro trifásico consiste en la instalación fija de dispositivos de dispositivos de protección a sobretensiones permanentes.
Arranque Estrella-Triángulo: Reducir el Pico de Corriente
Toda la teoría de tensiones y corrientes que hemos visto cobra vida en la aplicación industrial más famosa de estas conexiones: el arranque estrella-triángulo (Y- Δ) para motores asíncronos trifásicos.
A pesar del avance de los variadores de frecuencia y arrancadores suaves electrónicos, este método sigue siendo muy utilizado por su robustez, simplicidad y bajo coste.
Cuando conectamos un motor eléctrico directamente a la red (arranque directo), este se comporta inicialmente casi como un cortocircuito. En el instante t = 0, el motor está parado y no hay fuerza contraelectromotriz. La corriente de arranque (Iarr) se dispara entre 5 y 8 veces la corriente nominal (In).
Si el motor es grande, este pico de corriente provoca caídas de tensión en la red (las luces parpadean), puede disparar las protecciones (fusibles o magnetotérmicos) y somete a los bobinados y a la mecánica a un estrés térmico y mecánico severo.
Reducción de la Tensión en el Arranque Estrella Triángulo
La idea genial del arranque estrella-triángulo es usar la propia configuración de las bobinas para reducir la tensión durante los primeros segundos, sin necesidad de transformadores externos.
El proceso se divide en 2 etapas temporizadas:
● Etapa 1: Arranque en estrella (la reducción)
Inicialmente, mediante un juego de contactores, conectamos las bobinas del motor en estrella (Y).
Aunque nuestra red sea de 400 V (VL), al estar en estrella, cada bobina recibe internamente la tensión de fase: Vbobina = VF = 400 V / √3 ≈ 230 V. Por tanto, estamos alimentando el motor al 58% de su tensión nominal.
El resultado matemático (la Regla del 1/3) es que al reducir la tensión en √3, la corriente y el par motor se reducen cuadráticamente.
Iarranque (Y) = (1/3) · Iarranque (Δ)
Parranque (Y) = (1/3) · Parranque (Δ)
En resumen: el motor arranca suavemente, consumiendo 3 veces menos corriente.
● Etapa 2: Conmutación a triángulo (régimen nominal)
Pasados unos segundos (cuando el motor ya ha alcanzado el 70-80% de su velocidad nominal), un temporizador da la orden de cambio. Se desconecta la estrella y se conectan las bobinas en triángulo (Δ).
Ahora cada bobina queda conectada directamente entre 2 fases, siendo Vbobina = VL = 400 V. El motor recupera toda su fuerza, su par nominal y trabaja en su punto de diseño para mover la carga.
Circuitos de Fuerza y Mando para el Arranque Estrella Triángulo
Para realizar los esquema de potencia (fuerza) y maniobra (mando) se necesitan 3 contactores:
- KM1 (línea): alimenta el motor siempre.
- KM2 (estrella): une los finales de bobina (U2, V2, W2) creando el punto neutro (cortocircuito).
- KM3 (triángulo): conecta los finales con los principios en bucle.
Además, se suele usar un temporizador (KT1) para automatizar la transición de estrella a triángulo sin necesidad de intervención manual.
A continuación, se muestran los circuitos de fuerza y mando del arranque estrella-triángulo de un motor trifásico con temporizador.
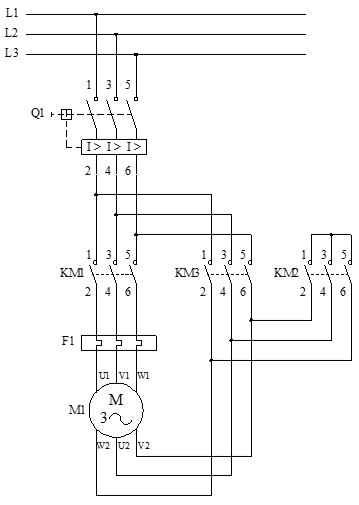
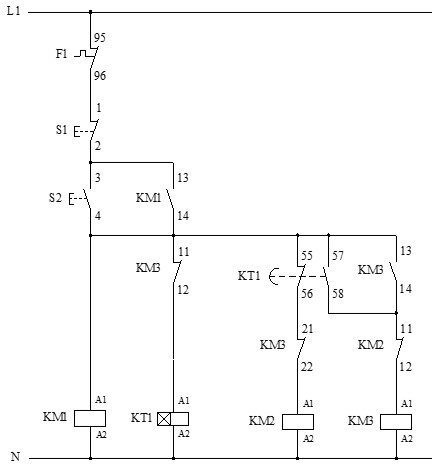
La secuencia de operación completa es la siguiente:
1º) Arranque en estrella (Y)
- Se activa el pulsador de marcha S2.
- KM1 (línea) → Alimentación principal al motor.
- KM2 (estrella) → Bobinas del motor en configuración Y.
- KT1 (temporizador) empieza a contar.
2º) Transición automática
- Cuando KT1 finaliza su temporización (típicamente 2-10 segundos):
- Desactiva KM2 (estrella).
3º) Funcionamiento en triángulo (Δ)
- KM3 (triángulo) → Bobinas del motor en configuración Δ.
- El motor continúa funcionando a plena potencia.
La protección a cortocircuitos del motor se realiza mediante el interruptor automático (Q1) y la protección a sobrecargas mediante el relé térmico (F1).
⚠️ Nota de Seguridad: Para realizar este arranque en una red estándar de 400 V, el motor debe ser 400/690 V. Si usamos un motor con placa 230/400 V, significa que sus bobinas están diseñadas para 230 V. Lo arrancaremos bien en estrella (230 V), pero al pasar a triángulo le meteremos 400 V a unas bobinas de 230 V. El motor se quemará en segundos.
También te puede interesar:

Condensador Eléctrico (Capacitor): Qué es, Tipos, Código y Fórmulas
Bobina o Inductor Eléctrico: Qué es, Símbolo y Funcionamiento (Ley de Lenz)
Generación de Corriente Alterna: El Alternador y la Inducción Electromagnética
Parámetros de la Onda Senoidal (CA): Frecuencia, Periodo y Valor Eficaz (RMS)
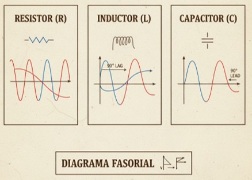
Receptores en Corriente Alterna: Circuitos R, L y C (Resistivo, Inductivo y Capacitivo)
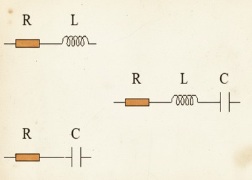
Circuitos Serie RL, RC y RLC: Impedancia, Fórmulas y Resonancia

Receptores en Paralelo (RLC): Cálculo de Corrientes y Potencias
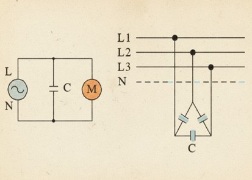
Factor de Potencia (cos φ) y Energía Reactiva: Qué es y Cómo Corregirlo