Fórmulas para el Cálculo de Armónicos

Un análisis eficaz de la calidad de la energía eléctrica requiere comprender en profundidad las fórmulas para el cálculo de armónicos, útiles para cuantificar la distorsión en señales de tensión y corriente presente en una red.

Estos parámetros constituyen herramientas fundamentales tanto para el diagnóstico como para la implementación de soluciones de mitigación, ya que facilitan la identificación de los armónicos dominantes y su contribución al deterioro de la calidad del suministro eléctrico.

El análisis de estos indicadores, como la distorsión armónica individual, la distorsión armónica total, el factor de potencia en presencia de armónicos, etc., resulta esencial para comprender la verdadera dimensión del problema y tomar decisiones acertadas en el diseño, operación y mantenimiento de las instalaciones eléctricas modernas.

Su correcta interpretación depende de un proceso riguroso de análisis y, sobre todo, de un preciso cálculo de armónicos.

Indicadores Fundamentales de la Distorsión Armónica

Para diagnosticar y comprender los armónicos, se deben utilizar métricas específicas que cuantifiquen la distorsión de una señal eléctrica. Estas métricas ofrecen una visión clara de cómo una onda se desvía de su forma sinusoidal ideal.

Factor de Cresta (CF)

El factor de cresta (CF) es un indicador que compara el valor de pico de una señal con su valor eficaz o RMS. Se define como:

● Valor máximo: el valor de pico o máximo de una señal es la amplitud más alta que alcanza una onda, medida desde su punto de equilibrio o valor cero. En una onda sinusoidal, representa el punto más alto en la cresta o el más bajo en el valle.  Este valor sirve para determinar el límite de voltaje o corriente que un componente eléctrico puede soportar sin sufrir daños.

● Valor eficaz: el valor eficaz o RMS (del inglés Root Mean Square) de una señal de corriente alterna (AC) es el valor de corriente continua (DC) equivalente que produciría el mismo efecto de calentamiento en una resistencia. Para una onda sinusoidal pura, el valor RMS es el valor máximo dividido por √2.

Para una onda sinusoidal perfecta, la relación entre el valor máximo y el eficaz es constante. Sin embargo, las cargas no lineales, al consumir corriente en picos bruscos, hacen que la relación entre el pico y el valor eficaz aumente significativamente.

Por ejemplo, una corriente con un CF de 3 o 4 es una señal con una distorsión armónica considerable. Un CF alto es una señal de alerta inmediata de la presencia de armónicos.

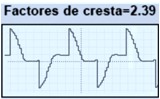
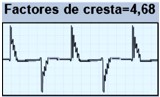
Valor Eficaz (RMS)

El valor eficaz o RMS (Root Mean Square), como ya se ha comentado, es la métrica que representa el equivalente en corriente continua (DC) que produciría el mismo efecto de calentamiento en una resistencia. Aunque es un concepto fundamental, la forma de medirlo es esencial en presencia de armónicos.

● Medidores de valor medio: estos medidores miden el valor promedio de la señal y luego lo multiplican por un factor de corrección (1,11 para una senoide perfecta) para estimar el valor eficaz. Esta técnica asume que la onda es perfectamente sinusoidal.

Cuando la señal está distorsionada, este factor de corrección es incorrecto, lo que lleva a lecturas significativamente erróneas que pueden estar fuera de un 50% del valor real. Esto explica por qué un fusible de 15 A puede fundirse cuando un medidor de valor medio solo indica 10 A: el valor eficaz real es mucho mayor de lo que el medidor es capaz de ver.

● Medidores de verdadero valor eficaz (True RMS): estos medidores utilizan circuitos electrónicos más avanzados que calculan el valor eficaz directamente a partir de la forma de onda real, sin hacer suposiciones sobre su forma.

Son los únicos instrumentos fiables para medir tensiones y corrientes en sistemas con armónicos. Para ser útiles, estos medidores también deben tener un factor de cresta especificado que indique el grado máximo de distorsión que pueden medir con precisión.

Estos medidores calculan el valor eficaz verdadero mediante la raíz cuadrática media o raíz cuadrada de la suma de cuadrados de todas las componentes armónicas. Este proceso es matemáticamente análogo al teorema de Pitágoras, ya que las diferentes frecuencias son ortogonales (independientes entre sí). Los valores eficaces de la tensión o la intensidad se obtienen así:

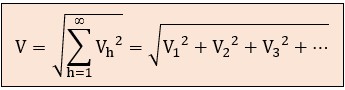
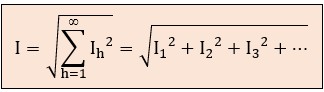
Ancho de Banda del Medidor

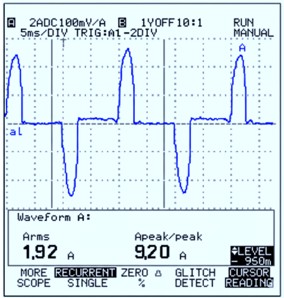
El ancho de banda de un medidor se refiere al rango de frecuencias que es capaz de procesar con precisión.

Si una señal distorsionada contiene armónicos de alta frecuencia (por ejemplo, el 13º armónico a 650 Hz en una red de 50 Hz), un medidor con un ancho de banda limitado (por ejemplo, 50 Hz o 60 Hz) no será capaz de captar estas componentes. En consecuencia, su lectura será errónea, incluso si se trata de un medidor True RMS con un bajo ancho de banda.

Para un diagnóstico preciso en entornos industriales, se requieren medidores con un ancho de banda lo suficientemente amplio, generalmente por lo menos de 1 kHz, para capturar los armónicos de órdenes más altos que son comunes.

Principales Fórmulas para el Cálculo de Armónicos

Para cuantificar el nivel de armónicos en una red, se utilizan métricas estandarizadas que ofrecen una visión clara y comparable de la distorsión. Estas métricas permiten evaluar la calidad de la energía y diagnosticar la severidad de un problema.

Distorsión Armónica Individual (IHD)

La distorsión armónica individual (IHD) o distorsión armónica de orden h, es una medida que evalúa la magnitud de un armónico específico con relación a la frecuencia fundamental.

Esta métrica identifica qué corriente armónica en particular es la más dominante o problemática en un sistema. Al analizar los valores de IHD, se puede determinar si la distorsión es causada por un tipo específico de carga no lineal. Por ejemplo, una alta IHD del 5º o 7º armónico es común en sistemas de variadores de velocidad.

La distorsión armónica individual existe tanto en tensión como en corriente. Se expresan como un porcentaje y se calculan para cada orden armónico (h).

● Distorsión armónica individual de tensión v_h (%): mide cuánto representa un armónico de orden h (V_h) respecto al valor eficaz de la tensión fundamental (V₁), en porcentaje.

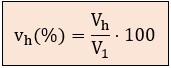
Por ejemplo, si la fundamental V₁ = 230 V y el 5º armónico es V₅ = 11,5 V,

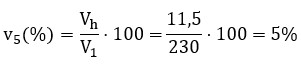
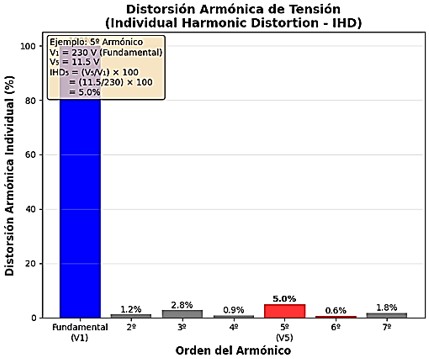
Cuando se habla de calidad de la tensión de suministro, se evalúan los valores de v_h(%), pues la norma IEC 61000-2-2 fija límites.

● Distorsión armónica individual de corriente i_h (%): mide la proporción de un armónico de orden h (I_h) respecto al valor eficaz de la corriente fundamental (I₁), en porcentaje.

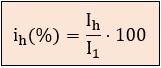
Por ejemplo, si la fundamental I₁ = 100 A y el 3º armónico es I₃ = 15 A,

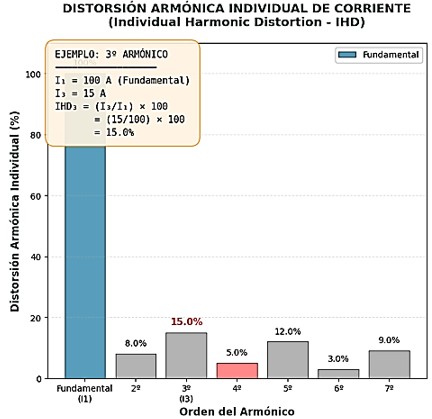
Cuando se evalúan las cargas no lineales y su impacto, se miden los valores de i_h(%) porque estas cargas inyectan corrientes armónicas en la red.

Distorsión Armónica Total (THD)

La distorsión armónica total (THD) es el indicador más importante y ofrece una medida global de toda la distorsión armónica presente en una señal. Se define como la relación entre el valor eficaz de todos los armónicos (excluyendo la fundamental) y el valor eficaz de la fundamental. Se expresa en porcentaje.

● Distorsión armónica total de tensión THD_V (%): es un indicador del efecto de la distorsión. Un alto THD_V significa que la tensión de la red está severamente deformada, lo que puede afectar a todos los equipos conectados. Su fórmula general es:

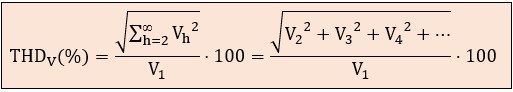
● Distorsión armónica total de corriente THD_I (%): es un indicador de la causa de la distorsión. Un alto THD_I indica que las cargas conectadas están extrayendo una corriente muy distorsionada de la red.

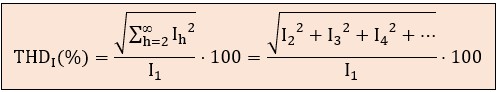
En una instalación típica, las cargas no lineales generan una alta THD_I, y esta corriente armónica, al pasar por la impedancia de la red, provoca una THD_V en el punto de acoplamiento común.

Por esta razón, un análisis completo de armónicos debe considerar ambos valores. Los estándares de calidad de energía, como la IEEE 519, establecen límites máximos para el THD_V y el THD_I para garantizar el buen funcionamiento de los sistemas eléctricos.

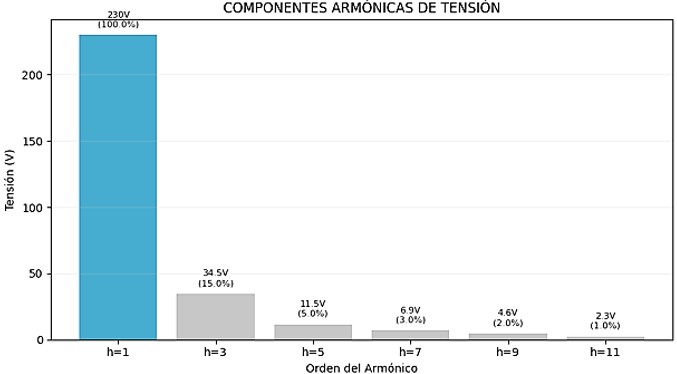
Por ejemplo, en el siguiente gráfico se obtiene la tasa de distorsión armónica total de tensión THD_V de una onda senoidal distorsionada, que corresponde al 16,25%. Cada componente armónica se representa mediante barras que muestran la magnitud de cada armónica eléctrica y su porcentaje respecto a la fundamental.

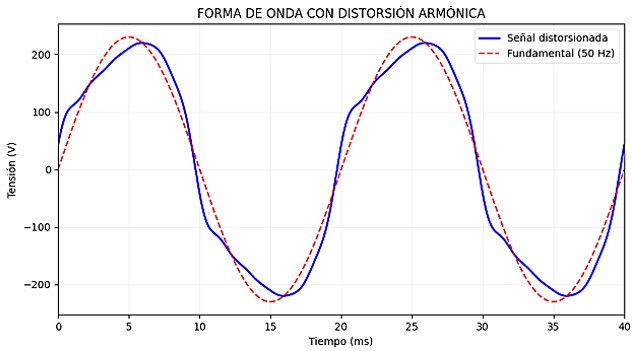
A continuación, se muestra la gráfica con la forma de onda distorsionada, donde se compara la señal fundamental pura y la señal con distorsión armónica con THD_V = 16,25%.

El Factor de Potencia en Presencia de Armónicos

Cuando la energía eléctrica es ideal, el factor de potencia (FP) se reduce a una simple relación entre la potencia activa y la potencia aparente, influenciada únicamente por el desfase entre la tensión y la corriente. Sin embargo, en presencia de armónicos, este concepto se vuelve mucho más complejo.

Distinción entre Coseno de Phi y Factor de Potencia con Distorsión

En un sistema sin armónicos, el factor de potencia es igual al coseno del ángulo de desfase (cos φ) entre la tensión y la corriente. Este ángulo solo considera la componente de la frecuencia fundamental (50/60 Hz). Las cargas inductivas o capacitivas causan un desfase que reduce el cos φ, pero la forma de onda permanece sinusoidal.

La fórmula del factor de potencia sin distorsión relaciona la potencia activa y la potencia aparente:

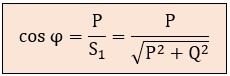
Sin embargo, cuando las cargas no lineales introducen armónicos, la corriente deja de ser sinusoidal. En este escenario, el factor de potencia verdadero o total se convierte en la métrica correcta, puesto que añade la potencia de distorsión (D).

El FP total incluye la distorsión de la forma de onda, mientras que el cos φ la ignora. Es por esto que un equipo con un factor de potencia bajo podría no tener una carga reactiva significativa, sino una alta distorsión armónica.

Componentes de la Potencia Eléctrica en un Sistema con Armónicos

En un sistema con armónicos, la potencia aparente total (S_T) no solo se compone de la potencia activa (P) y la potencia reactiva (Q), sino que también incluye una tercera componente conocida como potencia de distorsión (D). Esta potencia de distorsión no contribuye al trabajo útil, pero sí consume capacidad del sistema. La relación se describe como:

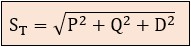
– Potencia activa (P): es la potencia que realiza trabajo útil (por ejemplo, calentar una resistencia, mover un motor). Se mide en vatios (W).

– Potencia reactiva (Q): es la potencia que se intercambia entre la fuente y las cargas inductivas o capacitivas (necesaria para magnetizar motores y transformadores). Se mide en voltios-amperios reactivos (VAR).

– Potencia de distorsión (D): es una potencia que no realiza trabajo y se genera exclusivamente por la presencia de armónicos en el sistema. Se mide en voltios-amperios de distorsión (VA).

En la ingeniería eléctrica tradicional, el triángulo de potencias se representa en 2 dimensiones, relacionando la potencia activa (P), la potencia reactiva (Q) y la potencia aparente (S1). Sin embargo, cuando se consideran los armónicos, el triángulo de potencias se representa en 3 dimensiones. El modelo tridimensional se conoce como el triángulo de potencias de distorsión:

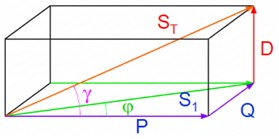
Este triángulo de potencias tridimensional es necesario porque la potencia de distorsión (D) no es ni activa ni reactiva en el sentido tradicional. Ignorarla daría una imagen incompleta del consumo de energía y de las pérdidas en el sistema.

En el triángulo de potencias de distorsión se observa que la suma vectorial de las 3 potencias (P, Q y D) conforman la potencia aparente total (S_T).

Relación entre el FP y el THD de la Corriente

En presencia de armónicos será el factor de potencia FP medido menor que el cos φ a causa de la distorsión, siendo:

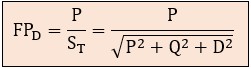
Suponiendo que el voltaje de la alimentación sea senoidal (el que proporciona la compañía suministradora) y que la corriente I quede distorsionada por el usuario, de forma que:

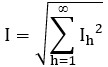
entonces el FP distorsionado es:

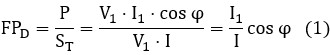
y tomando el THD_I en tanto por uno:

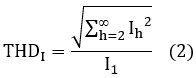
se obtiene operando matemáticamente con ambas expresiones:

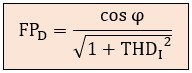
Esta fórmula demuestra que incluso si el desfase φ es cero (es decir, cos φ = 1, como en el caso de una resistencia pura), un alto THD_I reducirá el FP.

Una primera indicación de la presencia de armónicos en una instalación es cuando el FP medido es significativamente menor que el cos φ calculado.

Esto significa que la distorsión, y no solo el desfase reactivo, está reduciendo la eficiencia de la red, lo que lleva a un mayor consumo de energía aparente y, por lo tanto, a una menor eficiencia general. La gestión de armónicos es, en esencia, una forma de mejorar el factor de potencia total de una instalación.

Ejercicios Resueltos de Cálculo de Armónicos

A continuación, se presentan 8 ejercicios resueltos para practicar con las fórmulas para el cálculo de armónicos en las instalaciones eléctricas.

Ejercicio 1: Cálculo de armónicos

Ejercicio 2: Cálculo de armónicos

Ejercicio 3: Cálculo de armónicos

Ejercicio 4: Cálculo de armónicos

Ejercicio 5: Cálculo de armónicos

Ejercicio 6: Cálculo de armónicos

Ejercicio 7: Cálculo de armónicos

Ejercicio 8: Cálculo de armónicos

También te puede interesar:

Qué son los Armónicos Eléctricos

Origen de los Armónicos Eléctricos

Efectos de los Armónicos Eléctricos

Medida de la Distorsión Armónica

Resonancia y Distorsión Armónica

Filtrado de Armónicos Eléctricos