¿Qué son los Armónicos Eléctricos? Definición y Tipos
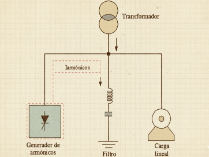
Los armónicos son voltajes y corrientes con frecuencias múltiplos de la fundamental, generados por cargas no lineales (como ordenadores o LEDs) que deforman la onda senoidal perfecta, causando calentamiento y fallos en la red.
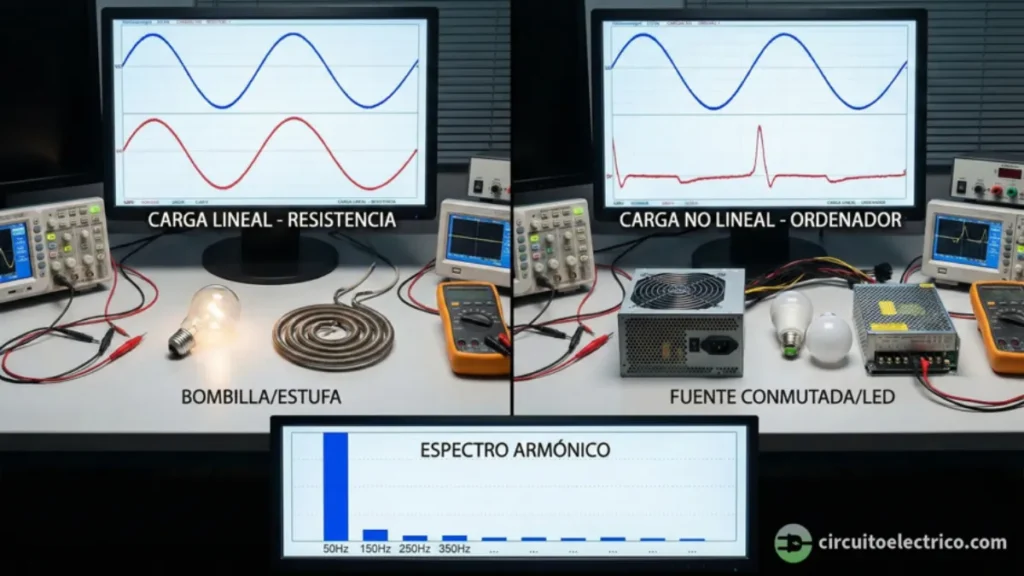
La presencia de armónicos en un sistema de CA provoca la deformación de las ondas de tensión y corriente. Estas pierden su característica forma senoidal pura, transformándose en ondas distorsionadas que evidencian la suma de múltiples frecuencias.
El suministro eléctrico ideal de las centrales generadoras es una onda perfectamente sinusoidal, con una frecuencia única y estable, como 50 Hz en Europa o 60 Hz en América. Esta pureza garantiza el funcionamiento óptimo de los equipos y la máxima eficiencia en la transmisión.
La onda sinusoidal permite que dispositivos, como transformadores y motores, funcionen de manera predecible, sin sobrecalentamiento ni estrés mecánico. En este entorno, los cálculos de potencia y el diseño de la red son sencillos y directos, ya que la corriente consumida es proporcional y sigue la misma forma de onda que la tensión.
Sin embargo, en las últimas décadas, la miniaturización de la electrónica y la necesidad de un control más preciso de la energía, ha dado lugar a la electrónica de potencia. Estos equipos extraen la corriente en pulsos de alta amplitud y muy corta duración, en lugar de hacerlo de manera continua y proporcional al voltaje, haciendo necesario el cálculo de armónicos para evaluar su impacto.
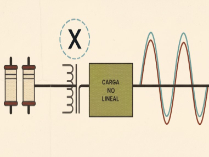
El resultado es que, aunque la tensión suministrada por la red pueda seguir siendo prácticamente sinusoidal, la corriente consumida por estas cargas no lineales es muy diferente. Y, por la propia naturaleza de la impedancia de la red, esta corriente no sinusoidal deforma la onda de tensión en el punto de conexión.
Contenidos
Definición: Frecuencia Fundamental y Múltiplos
Los armónicos en electricidad son componentes sinusoidales de una señal periódica cuyas frecuencias son múltiplo entero de la frecuencia fundamental del sistema.
En un sistema de energía eléctrica, la frecuencia fundamental es la frecuencia de la red (50 Hz o 60 Hz), que es la principal responsable de transferir la energía útil. El concepto de "múltiplo entero" es lo que clasifica a cada armónico y le da su nombre. Este múltiplo se conoce como el orden o rango armónico.
El orden armónico (h) es simplemente el número entero que multiplica a la frecuencia fundamental (f1) para obtener la frecuencia del armónico (fh). La relación matemática es:
Considerando una red eléctrica con una frecuencia fundamental de 50 Hz, los armónicos se nombran y calculan de la siguiente manera:
– Primer armónico (h = 1): es la frecuencia fundamental, la componente principal de la onda:
f1 = 1 · 50 Hz = 50 Hz.
– Segundo armónico (h = 2): es la componente con frecuencia del doble de la fundamental.
f2 = 2 · 50 Hz = 100 Hz.
– Tercer armónico (h = 3): su frecuencia es tres veces la fundamental.
f3 = 3 · 50 Hz = 150 Hz.
Y así sucesivamente. Aunque teóricamente los armónicos podrían existir hasta el infinito, en la práctica, su amplitud disminuye rápidamente a medida que el orden aumenta. Por lo general, se presta especial atención a los armónicos más bajos (como el 3º, 5º, 7º, etc.) ya que suelen ser los más significativos en amplitud y efectos negativos.
Es importante destacar que la presencia de ciertos armónicos depende del tipo de carga no lineal. Por ejemplo, las cargas monofásicas suelen generar armónicos impares (3º, 5º, 7º), mientras que en los sistemas trifásicos, la cancelación de ciertos armónicos es un factor relevante.
Cargas Lineales
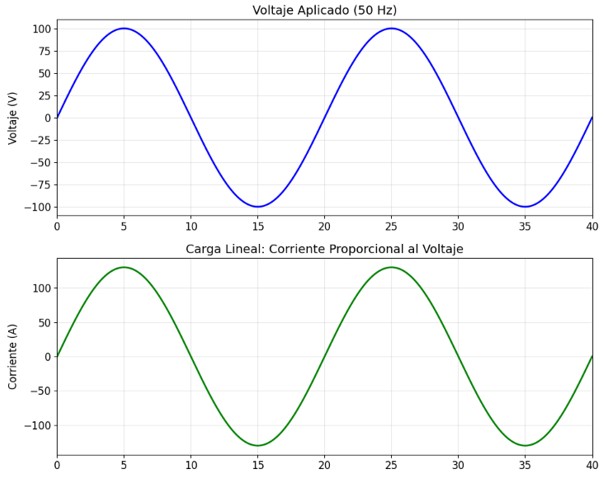
Una carga lineal es aquella en la que la corriente que consume es directamente proporcional a la tensión aplicada. Ejemplos clásicos son:
– Resistencias puras: un calentador o una bombilla incandescente. Si la tensión es sinusoidal, la corriente también lo es, y ambas señales están en fase.
– Motores de inducción y transformadores: estos dispositivos, aunque pueden desfasar la corriente con respecto a la tensión (debido a su naturaleza inductiva), mantienen la forma de onda sinusoidal de la corriente.
Cargas No Lineales
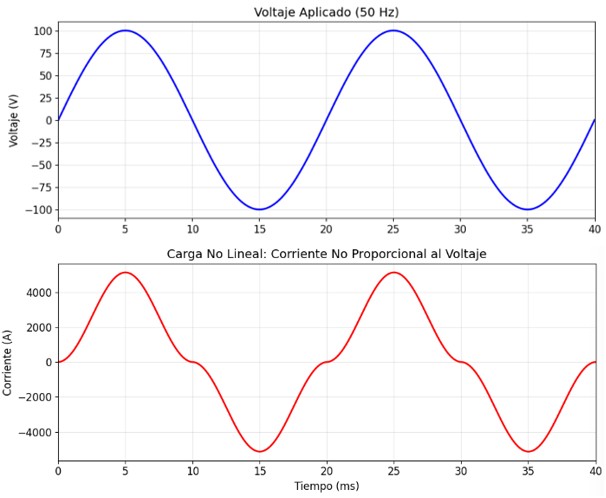
Una carga no lineal es aquella que no mantiene una relación constante entre la tensión y la corriente. En lugar de consumir una corriente suave y continua a lo largo de todo el ciclo de la onda de tensión, la extraen en impulsos bruscos y cortos.
El principal motor detrás de este cambio son los dispositivos con electrónica de potencia. Estos equipos utilizan rectificadores para convertir la corriente alterna (AC) de la red en corriente continua (DC), necesaria para el funcionamiento de sus componentes electrónicos internos. Ejemplos cotidianos de estas cargas son:
– Fuentes de alimentación conmutadas (SMPS): presentes en ordenadores, televisores, impresoras y la mayoría de los electrodomésticos modernos.
– Sistemas de iluminación LED: sus controladores electrónicos rectifican la corriente de entrada.
– Variadores de frecuencia (VFD): utilizados para controlar la velocidad de motores en la industria.
– Cargadores de vehículos eléctricos: son esencialmente grandes rectificadores.
– Sistemas de energía solar fotovoltaica y eólica: sus inversores convierten la corriente DC de los paneles o aerogeneradores en corriente AC para inyectarla en la red.
La suma de los impulsos de corriente de miles de estos dispositivos deforma la onda sinusoidal de la red en todo su conjunto, creando la aparición de los armónicos.
Teoría Matemática: Descomposición de Fourier
La serie de Fourier revela que cualquier señal periódica, por compleja que sea, puede descomponerse en la suma de ondas sinusoidales puras. Esta descomposición muestra que la onda compleja está formada por una frecuencia fundamental más sus múltiplos armónicos con amplitudes específicas:
● La frecuencia fundamental: esta es la componente principal, la onda sinusoidal original. En los sistemas de potencia, esta es la onda de 50 Hz (o 60 Hz) que suministra la energía útil a los equipos.
● Armónicos: son componentes sinusoidales adicionales. La característica principal de estos armónicos es que sus frecuencias son múltiplos enteros de la frecuencia fundamental. Por ejemplo, en una red de 50 Hz, el segundo armónico tendrá 100 Hz, el tercero 150 Hz, el cuarto 200 Hz, y así sucesivamente.
La serie de Fourier demuestra que la suma de la onda fundamental y sus armónicos reproduce exactamente la onda distorsionada original. Cada armónica eléctrica posee amplitud y fase específicas, cuya combinación genera la forma no sinusoidal característica.
Las cargas no lineales producen estos armónicos que se superponen a la fundamental de 50 Hz, creando distorsión. El análisis de Fourier permite cuantificar cada frecuencia armónica presente en la red, siendo esencial para diagnosticar y resolver problemas de calidad eléctrica.
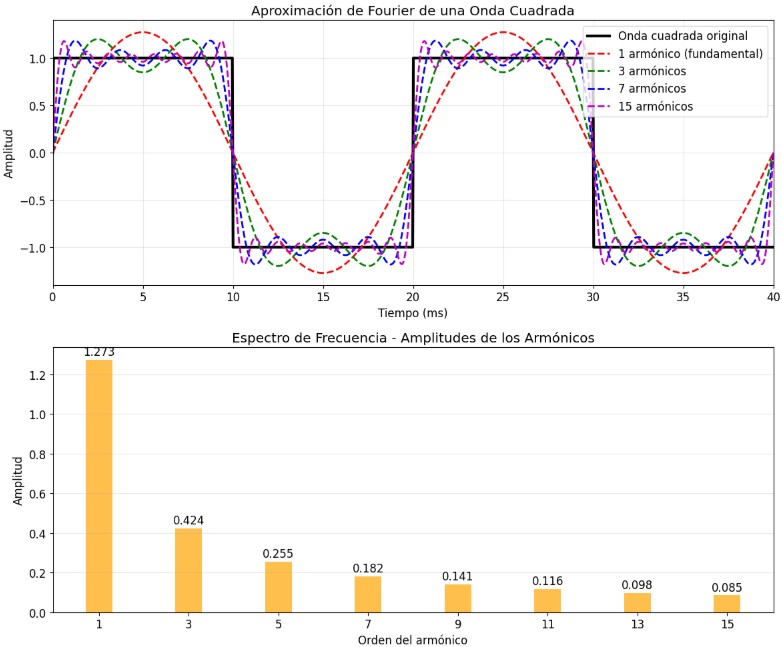
El siguiente gráfico ilustra cómo la Serie de Fourier descompone una onda cuadrada (negra) en componentes sinusoidales. La onda fundamental de 50 Hz (roja) es insuficiente para recrear la forma cuadrada. Al incorporar el tercer armónico de 150 Hz (verde) emergen los primeros escalones. La adición del séptimo armónico de 350 Hz (azul) acerca notablemente la forma a la onda cuadrada ideal.
La suma de todos los armónicos reproduce bastante bien la onda original, de forma que, cuantos más armónicos sumemos, más perfecta será la reconstrucción de la onda cuadrada.
Representación de los Armónicos Eléctricos
Para entender realmente el impacto de los armónicos, no basta con la teoría; hay que visualizarlos. Afortunadamente, existen dos maneras principales de representar una señal eléctrica, cada una de las cuales ofrece una perspectiva única sobre el problema de la distorsión armónica.
Representación Temporal de un Armónico
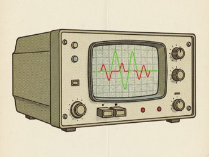
La representación temporal es la vista más intuitiva. Es lo que se vería en un osciloscopio, un instrumento que muestra la amplitud de una señal en función del tiempo. En un sistema ideal, esta representación sería una onda sinusoidal perfecta, suave y simétrica.
Sin embargo, cuando las cargas no lineales introducen armónicos, la forma de la onda cambia drásticamente. Lo que el osciloscopio muestra es la onda distorsionada resultante, que es la suma algebraica instantánea de la onda fundamental y todas las componentes armónicas.
Esta representación es muy útil para identificar visualmente si una señal está distorsionada, pero no nos dice qué armónicos específicos están causando el problema ni cuán potentes son.
Por ejemplo, en el siguiente gráfico de representación temporal de armónicas eléctricas, se representa una onda de 50 Hz (frecuencia fundamental, en color azul) de amplitud de 130 A y una onda de 150 Hz (tercer armónico, en color rojo) de amplitud 25 A. Se puede ver la onda que se observaría en el osciloscopio (onda deformada, en color verde).

Representación Espectral de un Armónico
La representación espectral nos da la información que la representación temporal oculta. En lugar de mostrar la señal en función del tiempo, un analizador de espectro muestra la amplitud de la señal en función de la frecuencia. Esto nos permite ver las componentes individuales que conforman la onda distorsionada.
La representación espectral es como el "ADN" de la señal. Se visualiza a menudo como un gráfico de barras. Cada barra vertical representa un armónico específico:
– La barra más alta, a 50 Hz, representa la amplitud de la frecuencia fundamental.
– Las siguientes barras se encuentran a 100 Hz (2º armónico), 150 Hz (3º armónico), 200 Hz (4º armónico), y así sucesivamente. La altura de cada barra indica la magnitud o "fuerza" de ese armónico en particular.
Esta representación permite diagnosticar la causa de la distorsión. Al observar las barras más altas, se pueden identificar qué armónicos son los más problemáticos. Por ejemplo, si la barra del 3º o el 5º armónico es particularmente alta, se puede inferir que la fuente del problema son cargas con rectificadores monofásicos o trifásicos.
En esencia, la representación espectral nos da la radiografía de la señal, permitiéndonos ver cada componente de forma individual y no solo la suma total.
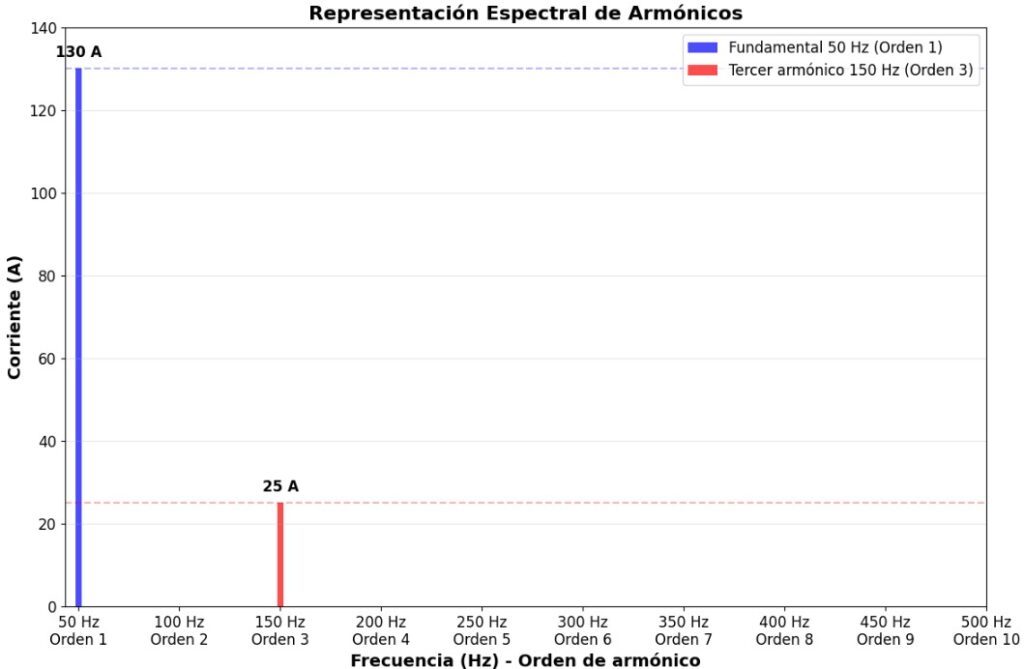
Por ejemplo, en el siguiente gráfico de representación espectral de armónicos se representa una onda de 50 Hz (frecuencia fundamental, en color azul) de amplitud de 130 A y una onda de 150 Hz (tercer armónico, en color rojo) de amplitud 25 A. Se puede ver la amplitud (altura) de cada uno, lo que nos da una idea de su magnitud.
Clasificación: Armónicos Pares e Impares
Una clasificación esencial para entender el comportamiento e impacto de los armónicos, los divide en 2 grupos: armónicos eléctricos pares e impares.
Armónicos Impares
Son los tipos de armónicos más comunes en los sistemas eléctricos y aparecen cuando una carga no lineal introduce asimetrías en la forma de onda, pero manteniendo cierta periodicidad en relación con la señal fundamental. Suelen ser dominantes en instalaciones industriales con gran presencia de convertidores electrónicos y rectificadores.
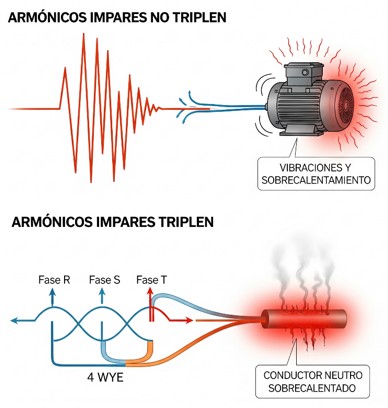
● Armónicos impares no triples: también denominados armónicos no triplen, como el 5º (250 Hz), 7º (350 Hz), 11º (550 Hz), 13º (650 Hz), etc., son los más comunes en las cargas no lineales monofásicas y trifásicas, como los convertidores de frecuencia y los variadores de velocidad. Su efecto principal es la distorsión de la forma de onda, que causa:
– Sobrecalentamiento en cables y transformadores debido al aumento de las pérdidas por efecto Joule (P = R · I2).
– Pares de torsión pulsantes en motores, que causan vibraciones mecánicas, ruido y envejecimiento prematuro del aislamiento.
– Reducción de la vida útil de los equipos y la posibilidad de fallos.
● Armónicos impares triples: también denominados armónicos triplen, son los múltiplos de 3, como el 3º (150 Hz), 9º (450 Hz), 15º (750 Hz), etc. Son problemáticos en sistemas trifásicos de 4 hilos (tres fases y un neutro), que son comunes en edificios de oficinas y centros de datos.
Los armónicos triplen (3º, 9º, 15º...) son peligrosos porque, a diferencia de los demás, sus corrientes no se cancelan en el sistema trifásico, sino que se suman en el conductor neutro. Esto genera una sobrecarga severa que puede causar su sobrecalentamiento, derretir el aislamiento y provocar un incendio.
A medida que el orden de los armónicos aumenta, su magnitud tiende a disminuir, pero los de orden alto (por encima del 25º) aún pueden causar problemas de comunicación y fallos en la electrónica sensible.
Armónicos Pares
Son los tipos de armónicos menos frecuentes en los sistemas eléctricos y aparecen cuando existe una asimetría fuerte en la señal, por ejemplo, debido a una saturación en los transformadores, un mal diseño en rectificadores o la presencia de fallos en equipos electrónicos. Se manifiestan en múltiplos pares de la frecuencia fundamental (2º, 4º, 6º, 8º, etc.).
– Saturación de núcleos magnéticos: en transformadores o reactores que operan cerca o más allá de su punto de saturación, la curva de magnetización deja de ser simétrica, generando estos componentes.
– Fallos en circuitos electrónicos: un componente defectuoso en un rectificador (como un diodo en cortocircuito o abierto) o en un variador de frecuencia rompe la simetría de la conmutación.
– Desbalances de voltaje severos: las asimetrías importantes en la tensión de alimentación entre fases pueden provocar que los equipos electrónicos consuman corriente de manera desigual, generando armónicos pares.
Aunque su magnitud suele ser muy inferior a la de los armónicos impares, la detección de armónicos pares nunca debe subestimarse. Su presencia actúa como una señal de alarma que indica una condición anormal o un fallo incipiente en una carga.
Por lo tanto, la medición de armónicos pares es una herramienta valiosa de diagnóstico predictivo, que sugiere la necesidad inmediata de inspeccionar, mantener o reemplazar el equipo defectuoso para prevenir una fallo mayor. Ignorarlos puede permitir que el problema subyacente se agrave, derivando en paradas no planificadas o daños costosos.

Importancia de Entender los Armónicos
Comprender los armónicos eléctricos es una necesidad fundamental en el contexto energético actual. La proliferación de dispositivos con electrónica de potencia ha transformado los armónicos en un fenómeno omnipresente.
Por lo tanto, el análisis y la gestión de los armónicos han pasado a ser un pilar fundamental en la ingeniería eléctrica actual. El conocimiento de los armónicos es esencial por varias razones:
– Eficiencia energética: los armónicos causan pérdidas adicionales en forma de calor en los conductores, transformadores y motores. Este calor desperdicia energía, lo que se traduce en mayores costes operativos y una menor eficiencia general del sistema.
– Fiabilidad del equipo: la distorsión armónica puede provocar sobrecalentamiento y estrés en los componentes eléctricos, acortando su vida útil y aumentando el riesgo de fallos inesperados. Esto es especialmente crítico en entornos industriales y centros de datos, donde un fallo puede detener la producción o causar la pérdida de información crítica.
– Seguridad del sistema: la posibilidad de resonancia armónica es un riesgo significativo. Cuando las frecuencias de los armónicos coinciden con la frecuencia de resonancia natural del sistema, la tensión y la corriente pueden amplificarse peligrosamente. Esto puede causar daños catastróficos, fallos de equipo e incluso incendios.
– Compatibilidad y medición: los armónicos pueden interferir con equipos sensibles, como sistemas de control, medidores inteligentes y equipos de protección, provocando lecturas incorrectas y mal funcionamiento. Una red con alta distorsión armónica es un entorno impredecible en el que la medición precisa y el control fiable se vuelven muy difíciles.
En resumen, la comprensión de los armónicos eléctricos pares e impares no solo es esencial para diagnosticar y resolver problemas, sino que también es fundamental para el diseño de infraestructuras energéticas más robustas, eficientes y fiables para el futuro.
También te puede interesar:

Origen de los Armónicos: Cargas No Lineales y Diferencia entre Corriente y Tensión

Efectos de los Armónicos Eléctricos: Sobrecalentamiento y Fallos
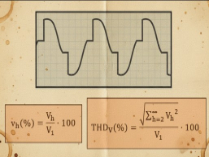
Fórmulas de Armónicos: Cálculo del THD y Factor de Cresta
Medida de Distorsión Armónica: Límites Máximos (THD) y Analizadores de Redes
Resonancia Armónica en Condensadores: Causas, Cálculo y Prevención