Cargas en Red Trifásica: Conexión, Equilibrado y Cálculo Total
Cuando abres un cuadro eléctrico industrial, rara vez encuentras un solo motor. Lo normal es enfrentarse a un ecosistema mixto: maquinaria pesada que consume corriente trifásica (400V) conviviendo con circuitos de iluminación y enchufes monofásicos (230V).
El desafío para el electricista no es solo conectar los cables, sino realizar el Cálculo de la Carga Total sin cometer el error de sumar amperios directamente.
En esta guía aprenderás a aplicar el Teorema de Boucherot, la importancia vital del Equilibrado de Fases para proteger el cable neutro y cómo dimensionar la línea principal que alimenta todo el sistema trifásico de corriente alterna.
Entre las cargas trifásicas típicas (conectadas entre las 3 fases) están los motores asíncronos para maquinaria y ventilación, compresores y sistemas de refrigeración industrial, hornos trifásicos de media y alta potencia o variadores de frecuencia que controlan motores trifásicos.
Las cargas monofásicas típicas (conectadas entre una de las fases y neutro) son la iluminación LED o fluorescente, tomas de corriente para ordenadores y equipos ofimáticos, sistemas de calefacción de baja potencia o equipos electrónicos y cargas no lineales diversas.
Contenidos
El Problema: Mezclar Motores (3F) y Luces (1F)
Ante esta mezcla de receptores, el técnico se enfrenta a una pregunta crítica: ¿Cuál es la potencia total que debo contratar y qué calibre de protección debo instalar?
Para dimensionar correctamente la sección del cable general de alimentación del cuadro y el calibre del Interruptor General Automático (IGA), necesitamos conocer con precisión la intensidad total de línea (IT) que circulará por la cabecera de la instalación. Un error en este cálculo puede derivar en 2 escenarios:
– Sobredimensionamiento: gastar dinero innecesario en cables de cobre de mayor sección de lo necesario y protecciones industriales más caras.
– Subdimensionamiento: el escenario peligroso. Provoca el disparo intempestivo de las protecciones (paradas de producción) o, peor aún, el sobrecalentamiento de los conductores por saturación.
Error Común: La Suma Aritmética
Aquí es donde muchos estudiantes y profesionales con poca experiencia cometen el error más grave en corriente alterna. La intuición nos dice que si tenemos un motor que consume 10 A y unas luces que consumen 5 A, la corriente total será 15 A.
¡Cuidado! En Corriente Alterna, 10 A + 5 A ≠ 15 A (salvo excepciones muy concretas).
¿Por qué ocurre esto? Porque la corriente alterna es una magnitud vectorial que tiene módulo (la cantidad de amperios) y argumento (el desfase o ángulo φ).
– No se pueden sumar aritméticamente las intensidades (I): dependiendo del factor de potencia de cada carga, las ondas de corriente no alcanzan sus picos al mismo tiempo.
– No se pueden sumar aritméticamente las potencias aparentes (S): 10 kVA + 5 kVA casi nunca resultan en 15 kVA.
Sumar directamente los amperios de varias cargas con diferente factor de potencia es como intentar sumar la velocidad de dos personas que corren en direcciones distintas: el resultado no es la suma de sus velocidades, sino la resultante vectorial.
El Método de las Potencias
Para resolver este problema con precisión matemática, debemos recurrir a la geometría y a la trigonometría. El procedimiento estándar establece que, aunque no podemos sumar las potencias aparentes (S) ni las intensidades (I) directamente, sí podemos sumar sus componentes:
- Las potencias activas (P) se suman aritméticamente (kW con kW).
- Las potencias reactivas (Q) se suman algebraicamente (kVAR inductivos restan o suman con kVAR capacitivos).
Nuestro objetivo será aprender a descomponer cada carga, sumar sus componentes y utilizar el Teorema de Pitágoras para reconstruir el Triángulo de Potencias Total. Solo así obtendremos los 3 datos principales de la instalación:
● La potencia aparente total (ST): la carga real que soporta el transformador.
● El Factor de Potencia de la instalación (cos φT): para saber si necesitamos compensar con condensadores.
● La intensidad total (IT): el dato final para elegir nuestro cable y nuestro interruptor general.
El Triángulo de Potencias
Para abordar el cálculo de una instalación con múltiples receptores, debemos abandonar la aritmética simple y entrar en el terreno de la geometría vectorial. Así, en corriente alterna, la energía no fluye de una única forma; se manifiesta en 3 componentes distintas que se relacionan entre sí formando un triángulo rectángulo: el Triángulo de Potencias.
Entender este triángulo es fundamental porque es el "mapa" que utilizaremos para sumar las cargas. A continuación, desglosamos cada uno de sus lados.

Potencia Activa (P)
Es el cateto horizontal del triángulo. Representa la energía que realmente se transforma en trabajo útil. Es la potencia que "hace cosas": mueve el eje de un motor, calienta una resistencia o ilumina una lámpara.
Su unidad es el vatio (W) o kilovatio (kW). Es la proyección de la potencia total sobre el eje horizontal (real). La fórmula obtenida por trigonometría es:

Nota importante: Esta es la potencia que habitualmente se suma de forma directa (PT = P1 + P2 + P3 + ...) y es la que registran los contadores de energía básicos para la facturación de consumo activo.
Potencia Reactiva (Q)
Es el cateto vertical del triángulo. Esta energía no produce trabajo útil directo. Es una energía "fluctuante" que intercambian el generador y los receptores para crear los campos magnéticos (en bobinas/motores) o campos eléctricos (en condensadores) necesarios para el funcionamiento de los equipos.
Su unidad es el voltiamperio reactivo (VAR) o kilovoltiamperio reactivo (kVAR). Es la proyección sobre el eje vertical (imaginario). La fórmula obtenida por trigonometría es:

Aunque no produce trabajo, es vital calcularla porque ocupa espacio en los cables y transformadores, aumentando la corriente necesaria sin aportar potencia mecánica.
Potencia Aparente (S)
Es la hipotenusa del triángulo. Representa la potencia total que debe suministrar la fuente de alimentación (transformador) y que debe soportar la línea de transporte. Es la suma vectorial de las 2 anteriores.
Se mide en voltiamperios (VA) o kilovoltiamperios (kVA). Se obtiene mediante el Teorema de Pitágoras, ya que P y Q forman un ángulo de 90°. La fórmula es:

Trigonometría Aplicada al Cálculo
Para resolver problemas de instalaciones con varias cargas, rara vez nos dan el valor de Q o S directamente. Lo habitual es conocer la potencia activa (P) (placa del motor) y el Factor de Potencia (FP o cos φ).
Por lo tanto, necesitamos herramientas trigonométricas para "averiguar" los datos faltantes y poder dibujar el triángulo de cada carga.
La herramienta clave es la tangente (tan φ). Esta es la fórmula más útil para nuestros cálculos. Nos permite obtener directamente la potencia reactiva (Q) si conocemos la activa (P) y el ángulo.
Recordemos que:

De aquí despejamos la fórmula que usaremos repetidamente en el procedimiento de cálculo:
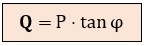
Para cada receptor de nuestra instalación, seguiremos este flujo lógico:
- Miramos el Factor de Potencia (FP) dado por el fabricante.
- Calculamos el ángulo φ usando el arco coseno: φ = arccos (FP).
- Calculamos la tan φ de ese ángulo.
- Obtenemos la potencia reactiva necesaria: Q = P · tan φ.
Con estos valores (P y Q) ya tendremos los 2 catetos listos para ser sumados con los de los otros receptores.
El Método de Boucherot (Suma de Potencias)
Para calcular una instalación trifásica con múltiples receptores, debemos aplicar el Método de Boucherot, que disecciona la instalación circuito por circuito.
El procedimiento estándar se basa en 3 pasos fundamentales que nos llevarán desde el detalle individual hasta la visión global de la instalación: análisis individual de cargas, suma de potencias y construir el triángulo de potencias total.
Análisis Individual de Cargas
El primer paso consiste en tratar cada receptor (motor, grupo de luces, horno, etc.) como un elemento aislado. Imaginemos que cada equipo tiene su propio "pequeño triángulo de potencias".
Para cada carga i conectada a la red, necesitamos extraer 2 datos fundamentales, que generalmente encontramos en la placa de características o en la ficha técnica:
- Potencia activa (Pi): expresada en vatios (W) o kilovatios (kW).
- Factor de Potencia (cos φi): un número adimensional entre 0 y 1.
Nuestro objetivo es hallar la potencia reactiva (Qi) de cada carga. Para ello, utilizamos la trigonometría básica que repasamos en el punto anterior:
1º) Hallar el ángulo de desfase: despejamos el ángulo a partir del factor de potencia.
φi = arccos (FPi)
2º) Calcular la potencia reactiva: usamos la tangente del ángulo calculado.
Qi = Pi · tan (φi)
Nota (signo de la reactiva): es fundamental asignar el signo correcto:
● Cargas inductivas: tienen una potencia reactiva Q positiva (+). El vector apunta hacia arriba en el triángulo. Son la gran mayoría en la industria: motores, transformadores, lámparas de descarga, etc.
● Cargas capacitivas: tienen una potencia reactiva Q negativa (–). El vector apunta hacia abajo. Pueden ser condensadores, algunos drivers LED, etc.
Al finalizar este paso, tendremos una lista desglosada de pares (P, Q) para cada máquina de la instalación.
Suma de Potencias
Una vez descompuestas todas las cargas en sus componentes horizontal (activa) y vertical (reactiva), calculamos la potencia total. La potencia del sistema trifásico será la suma de las potencias de sus componentes, pero respetando su naturaleza.
¿Por qué no sumamos las potencias aparentes (S)? Porque las potencias aparentes son vectores con diferentes direcciones (diferentes ángulos φ). Sumar S1 + S2 directamente es un error matemático grave.
En su lugar, realizamos 2 sumas independientes:
● Suma de potencia activa total (PT): dado que todas las potencias activas van en la misma dirección (eje real positivo), se realiza una suma aritmética:

● Suma de potencia reactiva total (QT): aquí realizamos una suma algebraica. Debemos tener cuidado con los signos si hay condensadores mezclados con motores. No obstante, generalmente sumaremos kVAR inductivos, por lo que el resultado será positivo:
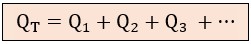
El Triángulo de Potencias Total
Ahora que hemos reducido toda la complejidad de la instalación a 2 únicos números grandes (PT y QT), podemos construir el Triángulo de Potencias de la Instalación.
Estos 2 valores son los catetos de nuestro triángulo final. Para encontrar la hipotenusa, que representa la potencia aparente total (ST), recurrimos al infalible Teorema de Pitágoras:
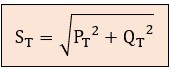
El valor resultante, ST (en kVA), es el dato real de la carga que "verá" el transformador y la acometida eléctrica. Con este valor, ya estamos listos para calcular la intensidad de línea y así poder dimensionar los cables.
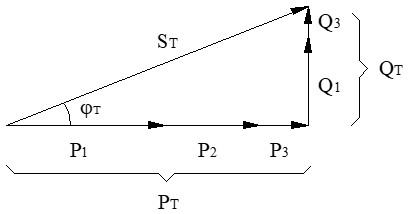
Por ejemplo, el triángulo total de potencias para 3 receptores sería el siguiente:
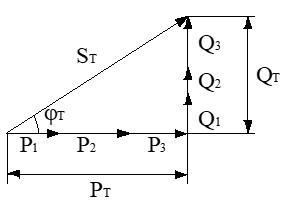
Obtención de los Parámetros Generales de la Instalación
Una vez que hemos construido el triángulo de potencias de la instalación, disponemos de los valores totales de la instalación: potencia activa total (PT), potencia reactiva total (QT) y potencia aparente total (ST).
Con estos datos, ya estamos en disposición de calcular los 2 parámetros finales que definirán la calidad y el dimensionamiento de nuestra instalación eléctrica.
Cálculo del Factor de Potencia Total
Aquí es necesario detenerse para desmentir uno de los errores conceptuales más frecuentes en el sector:
El Factor de Potencia total NO es el promedio de los factores de potencia de las cargas.
Si tienes un motor con cos φ = 0,8 y unas luces con cos φ = 1, el factor de potencia total no es 0,9. Calcularlo así ignora el "peso" (la potencia) que tiene cada carga en el sistema.
El Factor de Potencia real de la instalación es la relación trigonométrica final entre la potencia que realmente aprovechamos (PT) y la potencia total que suministra el transformador (ST). Se calcula proyectando el triángulo total:

La interpretación del resultado es la siguiente:
– Este valor nos indicará la "salud" de nuestra instalación.
– Si el resultado es bajo (por ejemplo, inferior a 0,9 o 0,95 dependiendo de la normativa local), la compañía eléctrica podría aplicar penalizaciones en la factura.
– Este dato es el que se utiliza para calcular, si fuera necesario, la batería de condensadores para la corrección del factor de potencia.
Cálculo de la Intensidad Total de Línea
Este es, posiblemente, el dato más importante para el instalador. La intensidad total es la corriente real que circulará por los conductores de la acometida o derivación individual y la que atravesará el Interruptor General Automático (IGA).
Para obtenerla, debemos "despejar" la corriente de la fórmula de la potencia aparente trifásica. Recordemos que S = √3 · VL · I. Por lo tanto:
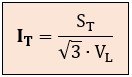
donde:
ST = es la potencia aparente total que hemos calculado por Pitágoras. ¡Atención a las unidades! Si ST está en kVA, debemos multiplicarla por 1.000 para pasarla a VA y obtener el resultado en Amperios.
√3 = es la constante de los sistemas trifásicos (≈ 1,732).
VL = es la tensión de línea (tensión entre fases). En la mayoría de instalaciones industriales estándar en Europa y gran parte de Latinoamérica, este valor es 400 V.
Esta intensidad IT es la base para consultar el Reglamento Electrotécnico para Baja Tensión (REBT o normativa local). Una vez se tiene la intensidad, se selecciona la sección del conductor (mm²) y se elige el calibre de las protecciones (fusibles o interruptores automáticos). Este proceso se puede consultar en cálculo de sección de conductores.
El Equilibrado de Fases: Evitar sobrecargar el Neutro
En una instalación industrial o comercial típica, la red de alimentación es trifásica (400 V entre fases), pero el consumo es híbrido. Tendremos grandes máquinas que requieren las 3 fases y multitud de pequeños receptores que se conectan entre fase y neutro (230 V).
¿Cómo integramos ambos tipos en nuestro cálculo general de potencia?
Receptores Trifásicos
Este es el caso más sencillo. Los motores, hornos industriales o grandes máquinas de climatización son cargas intrínsecamente equilibradas.
- Consumen la misma corriente de las 3 fases (L1, L2, L3).
- Se aplican directamente las fórmulas de P, Q y S que hemos visto en los apartados anteriores.
- Simplemente sumamos sus potencias al total acumulado (PT y QT).
Receptores Monofásicos en Red Trifásica
Aquí es donde el diseño de la instalación requiere mayor atención. Una carga monofásica se conecta entre una Fase y el Neutro.
Para realizar el cálculo global de la acometida, utilizamos el concepto de carga trifásica virtual equivalente. Esto se basa en la premisa del equilibrado de fases.
El Equilibrado Perfecto
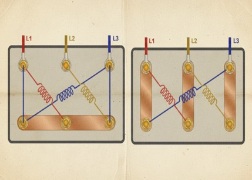
Imaginemos que tenemos 3 circuitos de iluminación monofásica idénticos (ej: 3 filas de luces de 1 kW cada una). Si conectamos inteligentemente:
- Fila “A” a la Fase L1.
- Fila “B” a la Fase L2.
- Fila “C” a la Fase L3.
Desde el punto de vista del transformador y del cable principal, el conjunto de estas 3 cargas monofásicas se comporta exactamente igual que una sola carga trifásica equilibrada de 3 kW.
– La potencia total: es la suma aritmética: PT = P1 + P2 + P3.
– La corriente por el conductor Neutro: es cero (las corrientes de retorno se anulan vectorialmente entre sí).
– Fórmula trifásica: podemos usar la fórmula trifásica general para calcular la intensidad de línea.
El Desequilibrio
En la práctica, es difícil conseguir un equilibrio perfecto (a veces encendemos las luces de la fase L1 pero no las de la fase L2). Si las cargas no están equilibradas:
– Aparece corriente en el Neutro: el vector resultante ya no es cero. Esto obliga a no reducir la sección del cable neutro.
– Dimensionamiento por la fase más cargada: para calcular la potencia contratada o el calibre del interruptor general, generalmente asumimos un reparto equitativo (PT/3) para estimar la corriente.
Sin embargo, si sabemos de antemano que habrá un desequilibrio fuerte (ej: una máquina monofásica muy potente y nada en las otras fases), el cálculo del cable debe hacerse basándose en la fase que soporta la mayor intensidad (el peor caso), y no en el promedio.
Para ver un caso práctico del desequilibrio producido por una carga monofásica, se puede consultar el Ejercicio 10 de sección de conductores en instalaciones interiores.
En resumen, para obtener la ST general, sumaremos todas las potencias activas y reactivas de las cargas monofásicas como si formaran un conjunto equilibrado. Esto nos dará la potencia total instalada. El instalador deberá, posteriormente, distribuir físicamente esas cargas en el cuadro para que la realidad se acerque lo más posible a este cálculo equilibrado.
Ejercicio Resuelto de Conexión de Receptores en Trifásica
Para consolidar todo lo aprendido, vamos a resolver un caso real paso a paso. Supongamos que debemos dimensionar la línea de alimentación para un pequeño taller que cuenta con los siguientes receptores conectados a una red trifásica de 400 V:
- Carga 1 (fuerza): un motor trifásico de 10 kW con un factor de potencia (cos φ) de 0,8.
- Carga 2 (calor): un horno industrial trifásico de resistencias de 5 kW. Al ser resistivo puro, su cos φ es 1.
- Carga 3 (iluminación): un conjunto de 150 lámparas LED repartidas equilibradamente en las tres fases, con una potencia por lámpara de 20 W y un cos φ de 0,9.
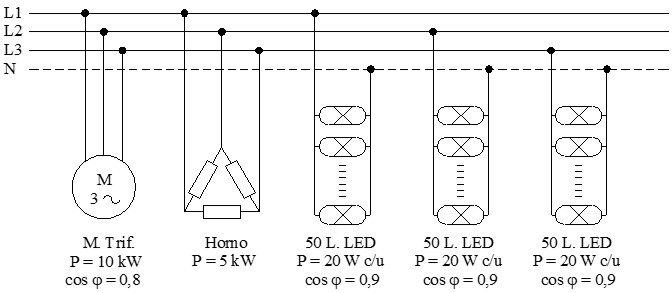
En el esquema se puede observar la distribución de las 150 lámparas de forma equitativa entre las 3 fases para que el sistema trifásico esté equilibrado. Como todas las lámparas son iguales, se distribuyen 50 lámparas en cada fase.
Análisis Individual (Descomposición de Cargas)
Nuestro primer objetivo es hallar la potencia reactiva (Q) de cada receptor. Para ello, necesitamos obtener el valor de la tan φ correspondiente a cada factor de potencia.
– Motor (P1 = 10 kW, cos φ= 0,8):
- Calculamos el ángulo: φ1 = arccos (0,8) = 36,87º.
- Obtenemos la tangente: tan (36,87º) = 0,75.
- Calculamos la potencia reactiva: Q1 = P1 · tan φ1 = 10 · 0,75 = 7,5 kVAR
– Horno (P2 = 5 kW, cos φ= 1):
- Calculamos el ángulo: φ2 = arccos (1) = 0º.
- Obtenemos la tangente: tan (0º) = 0.
- Calculamos la potencia reactiva: Q2 = P2 · tan φ2 = 5 · 0 = 0 kVAR
(Nota: las cargas resistivas puras no consumen energía reactiva).
– Iluminación (150 L. LEDs de 20 W, cos φ= 0,9):
- Obtenemos la potencia activa en lámparas: P3 = 150 · 20 W = 3.000 W = 3 kW
- Calculamos el ángulo: φ3 = arccos (0,9) = 25,84º.
- Obtenemos la tangente: tan (25,84º) = 0,484.
- Calculamos la potencia reactiva: Q3 = P3 · tan φ3 = 3 · 0,484 = 1,45 kVAR
Suma de Potencias
Ahora agrupamos las potencias según su naturaleza:
– Potencia activa total: PT = 10 + 5 + 3 = 18 kW
– Potencia reactiva total: QT = 7,5 + 0 + 1,45 = 8,95 kVAR
Triángulo de Potencias Total y Resultados
Con los catetos totales definidos, calculamos la hipotenusa (Potencia Aparente) y el resto de parámetros de la instalación.
– Potencia aparente total (ST): aplicamos Pitágoras:
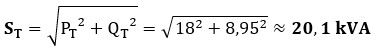
Observación: Si hubiéramos sumado las potencias aparentes individuales aritméticamente (S1 + S2 + S3), habríamos obtenido:
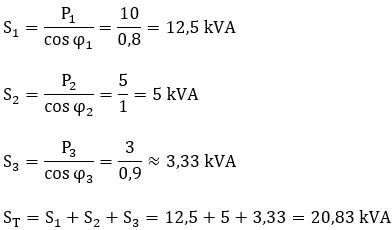
Aunque la diferencia parece pequeña, en grandes instalaciones este error implica sobrecostes importantes en transformadores
– Factor de Potencia de la instalación FPT:
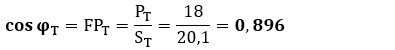
(Este valor es aceptable, aunque roza el límite de penalización en muchas normativas, lo que sugiere que podría ser necesario instalar una pequeña batería de condensadores).
– Intensidad de Línea (IT): finalmente, calculamos la corriente que pasará por el interruptor general. Recordamos usar VL = 400 V.
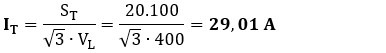
Conclusión: Para esta instalación, deberíamos dimensionar un cable capaz de soportar 29 A (probablemente un cable de 6 mm2 o 10 mm2 dependiendo de la longitud, sistema de instalación, caída de tensión máxima admisible, etc.) y una protección magnetotérmica acorde; en este caso, un interruptor automático de 32 A o regulable ajustado 29-30 A).
También te puede interesar:

Condensador Eléctrico (Capacitor): Qué es, Tipos, Código y Fórmulas
Bobina o Inductor Eléctrico: Qué es, Símbolo y Funcionamiento (Ley de Lenz)
Generación de Corriente Alterna: El Alternador y la Inducción Electromagnética
Parámetros de la Onda Senoidal (CA): Frecuencia, Periodo y Valor Eficaz (RMS)
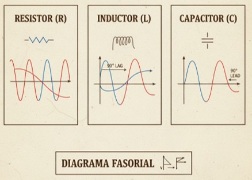
Receptores en Corriente Alterna: Circuitos R, L y C (Resistivo, Inductivo y Capacitivo)
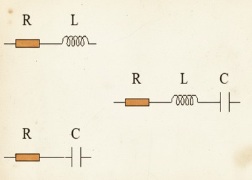
Circuitos Serie RL, RC y RLC: Impedancia, Fórmulas y Resonancia

Receptores en Paralelo (RLC): Cálculo de Corrientes y Potencias
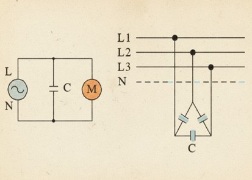
Factor de Potencia (cos φ) y Energía Reactiva: Qué es y Cómo Corregirlo