Receptores en Paralelo (RLC): Cálculo de Corrientes y Potencias
Mires donde mires, todo está en paralelo. Desde los enchufes de nuestra casa hasta la maquinaria de una industria, la conexión en paralelo es el estándar porque permite que todos los equipos reciban el mismo voltaje (ej: 230V) y funcionen independientemente.
Sin embargo, calcular la corriente total de la instalación no es tan simple como sumar los amperios de cada aparato. Debido al desfase que provocan motores (bobinas) y ordenadores (condensadores), debemos utilizar la Suma Vectorial o el Método de Boucherot (suma de potencias).
En esta guía aprenderemos a resolver estos circuitos paso a paso, prescindiendo de los números complejos, usando métodos gráficos o trigonométricos.
No obstante, en ingeniería aplicada, diseño o análisis avanzado, los números complejos son imprescindibles en el análisis de este tipo de circuitos de corriente alterna.
Contenidos
El Error Nº1: Suma Vectorial vs Aritmética
Dimensionar correctamente una instalación eléctrica implica responder a una pregunta fundamental: ¿Cuál es la intensidad total (IT) que debe soportar el cable principal y el interruptor automático de cabecera?
Si estuviéramos en un circuito de corriente continua (CC) o si todas nuestras cargas fueran puramente resistivas, la respuesta sería sencilla: aritmética pura. Por ejemplo, si tenemos una estufa que consume 10 A y otra que consume 5 A, el total son 15 A.
Sin embargo, en corriente alterna (CA), la realidad es más compleja debido a la naturaleza de las cargas:
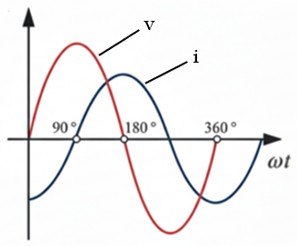
● Cargas resistivas: la corriente y la tensión van "de la mano" (en fase).
● Cargas inductivas (motores, transformadores, etc.): la corriente se retrasa respecto a la tensión.
● Cargas capacitivas (electrónica, condensadores, etc.): la corriente se adelanta respecto a la tensión.
Debido a estos desfases, no podemos realizar una suma aritmética directa de las intensidades. Sumar 10 A de un motor y 10 A de una estufa no da como resultado 20 A, sino un valor menor (vectorial). Ignorar esto lleva a cálculos erróneos y sobredimensionamiento de materiales.
Para resolver este problema con precisión técnica sin perdernos en matemáticas avanzadas, descartaremos el uso de números complejos (frecuente en ingeniería teórica) y optaremos por una herramienta mucho más visual e intuitiva: el Triángulo de Potencias.
Este método se basa en la trigonometría básica y el Teorema de Pitágoras. Al trabajar con potencias en lugar de intensidades directas, ganamos 2 ventajas enormes:
– Las potencias activas (P) se suman directamente: los vatios siempre se suman aritméticamente.
– Las potencias reactivas (Q) se suman algebraicamente: podemos restar los efectos capacitivos de los inductivos fácilmente.
A partir de este triángulo, obtendremos: la potencia total instalada, el factor de potencia resultante y, finalmente, la intensidad total real que circulará por la línea.
Conceptos Previos Fundamentales
Antes de adentrarnos en los cálculos trigonométricos, es vital entender la física que gobierna nuestro circuito. No podemos sumar "peras con manzanas"; en electricidad de corriente alterna, la naturaleza del aparato que conectamos define cómo se comporta la corriente.
La Conexión en Paralelo
En una instalación estándar, los receptores se conectan en paralelo. Esto significa que los bornes de cada aparato están conectados a los mismos 2 puntos de alimentación (Fase y Neutro).
● La tensión es común (V): todos los receptores "ven" el mismo voltaje. Si la línea es de 230 V, el motor, la lámpara y la estufa reciben 230 V. Por esta razón, usaremos la Tensión como nuestra referencia (ángulo 0º) para cualquier diagrama vectorial.
● La corriente se reparte (I): la intensidad total que sale de la fuente se divide entre los distintos caminos.
Nota: Según la Ley de Kirchhoff, la suma de las corrientes que entran en un nodo es igual a la suma de las que salen. Pero en corriente alterna, esta suma es vectorial, no aritmética.
Matemáticamente, esto se expresa como:
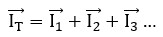
Tipología de Receptores
Para poder sumar estas corrientes (o potencias) correctamente, debemos clasificar cada aparato según cómo afecta al desfase entre la tensión y la intensidad. A este desfase lo llamamos ángulo φ (fi) y su coseno de conoce como Factor de Potencia (FP o cos φ).
Existen 3 "familias" de receptores:
● Receptores resistivos puros: transforman la electricidad íntegramente en calor o luz incandescente. Las resistencias no generan campos magnéticos ni eléctricos significativos.
Por ejemplo: estufas eléctricas, hornos de resistencia, planchas, bombillas incandescentes tradicionales, termos eléctricos, etc.
La corriente y la tensión están en fase. Alcanzan sus valores máximos y mínimos al mismo tiempo. Su FP es la unidad (cos φ = 1). Ángulo φ = 0º. No consumen potencia reactiva (Q = 0), solo potencia activa P.
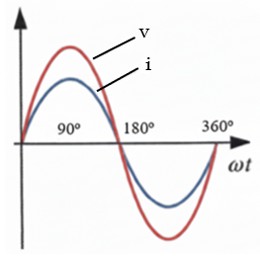
● Receptores inductivos: son la inmensa mayoría de las cargas industriales y domésticas motorizadas. Contienen bobinas que necesitan crear campos magnéticos para funcionar.
Por ejemplo: motores eléctricos, transformadores, reactancias de tubos fluorescentes, etc.
La bobina se opone a los cambios de corriente, provocando que la intensidad se retrase respecto a la tensión. Su FP es menor a 1, en retraso (cos φ < 1, inductivo). Generan potencia reactiva positiva (+Q).
● Receptores capacitivos: son menos frecuentes como cargas únicas, pero fundamentales para corregir instalaciones. Se comportan como "baterías" temporales que almacenan energía en un campo eléctrico.
Por ejemplo: condensadores, bancos de condensadores, y ciertas etapas de fuentes de alimentación electrónicas.
El condensador se opone a los cambios de tensión provocando que la intensidad se adelante respecto a la tensión. Su FP es menor a 1, en adelanto (cos φ < 1, capacitivo). Generan potencia reactiva negativa (-Q).

Resumen visual para el cálculo:
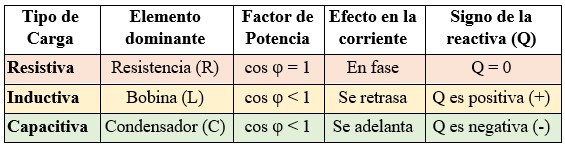
La tabla nos dirá si debemos dibujar el vector hacia la derecha (activa), hacia arriba (inductiva) o hacia abajo (capacitiva).
El Triángulo de Potencias
Como hemos visto, en corriente alterna las cargas no siempre consumen la energía de la misma manera. Así, para unificar estos comportamientos y poder realizar cálculos correctos sin recurrir a los complejos números imaginarios, podemos utilizar una representación gráfica universal: el triángulo de potencias.
Los Lados del Triángulo (H3)
El triángulo de potencias es un triángulo rectángulo. Cada uno de sus 3 lados representa una forma distinta de potencia: activa (P), reactiva (Q) y aparente (S).

● Potencia activa (P): es el cateto horizontal del triángulo.
Representa a la energía que realmente se transforma en trabajo útil (movimiento, calor, luz, etc.). Es la energía "útil", la que nos cobra la compañía eléctrica en la factura doméstica.
Se mide en vatios (W) o kilovatios (kW). La fórmula monofásica es:

Siempre se dibuja en el eje horizontal (eje X).
● Potencia reactiva (Q): es el cateto vertical del triángulo.
Es una energía que fluctúa entre la fuente y la carga. No produce trabajo útil directo, pero es indispensable para crear los campos magnéticos en motores y transformadores (o campos eléctricos en condensadores).
Se mide en voltiamperios reactivos (VAR) o kilovoltiamperios reactivos (kVAR). La fórmula monofásica es:

– Se dibuja en el eje vertical hacia arriba (positivo) si la carga es inductiva (motores).
– Se dibuja en el eje vertical hacia abajo (negativo) si la carga es capacitiva (condensadores).
● Potencia aparente (S): es la hipotenusa del triángulo.
Es la "suma vectorial" de las 2 anteriores. Representa la potencia total que la red eléctrica debe suministrar y que los cables deben soportar. Es el límite de capacidad de transformadores y generadores.
Se mide en voltiamperios (VA) o kilovoltiamperios (kVA). La fórmula monofásica es:

Es el lado más largo (hipotenusa), que une el origen de la potencia activa (P) con el final de la potencia reactiva (Q).
Relaciones Trigonométricas
Al formarse un triángulo rectángulo perfecto, podemos aplicar las reglas de la trigonometría básica. Estas fórmulas son las que usaremos para resolver la instalación.
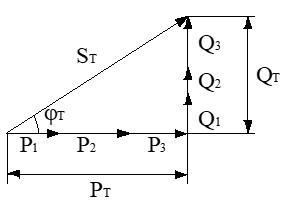
● Teorema de Pitágoras (para hallar la potencia total S): si conocemos la parte activa total (P) y la reactiva total (Q), podemos calcular la aparente (S) sin importar los ángulos individuales:

● El coseno (para hallar el Factor de Potencia FP): el ángulo φ que se forma entre la potencia activa (P) y la aparente (S) determina la eficiencia de la instalación.
– Si el ángulo φ es 0º, toda la potencia aparente se aprovecha como activa (eficiencia máxima).
– Cuanto mayor es el ángulo φ, más potencia reactiva tenemos (menos eficiencia).

● La tangente (para descomponer cargas): a menudo conocemos la potencia activa (P) de un motor y su cos φ, pero necesitamos saber su reactiva (Q) para poder sumarla. Usamos la tangente:
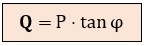
El triángulo de potencias nos enseña una verdad fundamental: la potencia aparente (S) siempre será mayor o igual a la potencia activa (P). Nuestro objetivo al diseñar o corregir una instalación es que el ángulo φ sea lo más pequeño posible, haciendo que S y P sean casi iguales (un cos φ cercano a 1).
El Método de Boucherot (Suma de Potencias)
Ahora que conocemos las potencias (P, Q y S), vamos a explicar el algoritmo para resolver cualquier circuito con varias cargas en paralelo. No intentaremos calcular la corriente total de golpe; primero analizaremos cada aparato por separado y luego unificaremos los resultados.
Vamos a desmontar cada carga eléctrica en sus componentes básicas (horizontal y vertical) para luego armar un gran "puzzle" final.
Recopilación y Normalización de Datos
Lo primero es hacer una lista de todos los receptores monofásicos a conectar en paralelo y asegurarnos de que tenemos los datos en las mismas unidades.
● Identificar la potencia: a veces el fabricante nos da la potencia activa (W o kW), otras veces la aparente (VA o kVA) y, en motores antiguos, a veces en caballos de vapor (CV o HP).
Conversión: 1 CV ≈ 736 W y 1 HP ≈ 746 W.
● Identificar el Factor de Potencia (FP o cos φ): es un número entre 0 y 1 que suele venir en la placa de características.
Cálculo de Potencias Parciales (Descomposición)
Para cada receptor (vamos a llamarlos carga 1, carga 2, etc.), necesitamos calcular su potencia activa (P) y su potencia reactiva (Q) individual.
1º) Hallar el ángulo de desfase (φ): con la calculadora científica, obtenemos el ángulo a partir del factor de potencia:
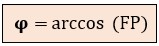
2º) Calcular la componente reactiva (Q): dependiendo del dato que tengamos de origen:
- Si conocemos P (W):
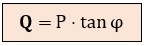
- Si conocemos S (VA):


¡Ojo con el signo!
– Si es un motor o iluminación (inductivo): la Q es positiva (+).
– Si es un condensador (capacitivo): la Q es negativa (–).
Sumar Todas las P (Activas)
El primer paso fundamental en el análisis de potencia de cualquier instalación eléctrica es obtener la sumatoria de potencias activas. Este procedimiento consiste en sumar la potencia activa consumida por cada receptor o carga conectada al sistema.
El proceso es sencillo en su concepción: sumamos aritméticamente todos los valores expresados en vatios (W). Esta suma directa es posible gracias a una característica esencial de las potencias activas: siempre son valores positivos y se suman, nunca se restan.
La razón que permite esta suma algebraica es que las potencias activas son vectores que actúan en la misma dirección. En el triángulo de potencias, la potencia activa se sitúa siempre sobre el eje horizontal. Como todos estos vectores comparten la misma dirección y sentido (positivo hacia la derecha), no existen ángulos o desfases entre ellos.
Matemáticamente, esto significa que podemos prescindir del tratamiento vectorial complejo para este cálculo específico. La potencia total PT se calcula mediante una simple suma algebraica:

Sumar todas las Q (Reactivas, restando bobina menos condensador)
Tras obtener la potencia activa total del sistema, el siguiente paso fundamental consiste en determinar la potencia reactiva total (QT).
Este cálculo presenta una diferencia esencial con el anterior: no se trata de una simple sumatoria de valores absolutos, sino de una suma algebraica cuidadosa de los voltiamperios reactivos (VAR), considerando rigurosamente sus signos.
La necesidad de considerar signos se deriva de la naturaleza dual de la energía reactiva, que puede ser de carácter inductivo (+) o capacitivo (-).
Los equipos más comunes en instalaciones industriales y comerciales, como motores, transformadores y balastos magnéticos, consumen potencia reactiva inductiva (tradicionalmente asignada con signo positivo), ya que requieren corriente para crear campos magnéticos.
Por el contrario, los condensadores o bancos de capacitores suministran potencia reactiva capacitiva (asignada con signo negativo), actuando como fuentes de este tipo de energía en el sistema.
Es precisamente en esta suma algebraica donde surge el principio fundamental de la compensación de potencia reactiva. Al sumar los valores positivos (consumo de los motores) con los valores negativos (generación de los condensadores), se produce un efecto de compensación parcial o total.

Este mecanismo es la base técnica de los sistemas de corrección del factor de potencia. Al instalar condensadores estratégicamente, se "alimenta" localmente la demanda reactiva de las cargas inductivas, reduciendo así la potencia reactiva total que debe suministrar la compañía eléctrica.
Cuando la compensación es exacta (QL = QC), el resultado neto es QT ≈ 0, logrando un factor de potencia cercano a la unidad.
Pitágoras para la S total (Triángulo de Potencias Total)
Ahora que tenemos los 2 catetos del gran triángulo de la instalación (PT y QT), aplicamos el Teorema de Pitágoras para hallar la hipotenusa. Esta es la potencia real que demandaremos al transformador.
⚠️ ¡Cuidado! Las potencias aparentes NO se pueden sumar aritméticamente entre sí. La potencia aparente de cada receptor incluye magnitud y ángulo de fase. Cuando sumamos cargas con diferentes factores de potencia, sus corrientes están desfasadas entre sí.
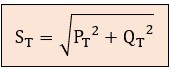
Por ejemplo, el triángulo total de potencias para 3 receptores sería el siguiente:
Resultados Finales: Factor de Potencia, Corriente y Desfase
Una vez que hemos "cerrado" nuestro triángulo total y conocemos los valores de potencia activa total (PT), reactiva total (QT) y aparente total (ST), estamos listos para responder a las preguntas prácticas del diseño eléctrico.
Ya no miramos los aparatos de forma individual; ahora observamos la instalación como un único bloque de carga conectado a la red.
El Factor de Potencia Total del Circuito con Receptores en paralelo
El primer indicador de salud de nuestra instalación es el Factor de Potencia resultante. Nos indica qué tan eficientemente está utilizando la energía el conjunto de la instalación.
El error más común es intentar calcular el FP total haciendo la media de los factores de potencia individuales. ¡Esto es incorrecto! El FP total es un promedio ponderado que surge de la relación vectorial.
Volviendo a la trigonometría básica, el coseno es el cateto adyacente dividido por la hipotenusa.

– Si el resultado es cercano a 1 (0,95 - 0,99): la instalación es muy eficiente. Casi toda la energía que circula se convierte en trabajo.
– Si el resultado es bajo (< 0,80): tenemos mucha energía reactiva circulando "inútilmente". Esto sobrecarga los cables y, en el caso de industrias, la compañía eléctrica cobrará una penalización económica.
La Intensidad Total del Circuito con Receptores en paralelo
Este es el dato más importante para el instalador. Es el valor que determinará la sección del cable y el calibre del Interruptor General Automático (magnetotérmico general).
Recordamos que la potencia aparente (S) es el producto de la tensión por la intensidad. Despejamos la intensidad usando el valor de ST que calculamos con Pitágoras.
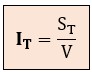
donde:
ST = potencia aparente total (en VA, no en kVA).
V = tensión de la red (ej. 230 V).
En caso de calcular la corriente con la potencia activa (PT), hay que recordar que la fórmula de la potencia activa monofásica incluye el cos φT.

⚠️ ¡Advertencia Importante! Al calcular la corriente total con la potencia activa (PT) nunca debemos hacerlo con la fórmula básica de la potencia (I = P/V) a menos que la carga sea 100% resistiva. Si lo hacemos en una instalación con motores, obtendremos un valor de corriente menor al real, lo que podría llevarnos a instalar un cable de menor sección que termine quemándose.
El Ángulo de Desfase Total del Circuito con Receptores en Paralelo
Aunque menos usado en la práctica diaria de instalación, conocer el ángulo total nos ayuda a visualizar el retraso global de la corriente respecto a la tensión.

Este ángulo es el que intentaríamos reducir si decidiéramos instalar una batería de condensadores para corregir el factor de potencia.
Ejercicio Resuelto con Receptores Monofásicos en Paralelo
Para asentar definitivamente la teoría, vamos a dimensionar una pequeña línea monofásica de taller. No usaremos números complejos, solo nuestra calculadora básica y el triángulo de potencias.
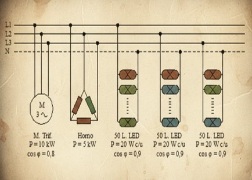
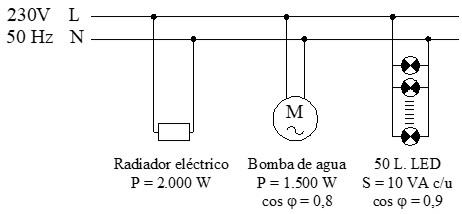
Tenemos una línea monofásica a 230 V (50 Hz) que alimenta simultáneamente a 3 receptores monofásicos conectados en paralelo:
– Receptor 1 (calefacción): un radiador eléctrico de 2.000 W (carga resistiva).
– Receptor 2 (fuerza): una bomba de agua con una potencia activa de 1.500 W y un factor de potencia de 0,8 (inductivo).
– Receptor 3 (iluminación): un conjunto de 50 luminarias LED. Cada lámpara con una potencia aparente de 10 VA y un factor de potencia de 0,9 (inductivo).
Calcular la potencia aparente total (ST), la intensidad total (IT) que debe soportar el cable y el Factor de Potencia total (cos φT) de la instalación.
Potencias Parciales (Descomposición)
Vamos a calcular la P (activa) y la Q (reactiva) de cada elemento por separado.
● Carga 1: el radiador (resistivo puro)
Al ser una resistencia, toda su potencia es activa. No consume reactiva.
– P1 = 2.000 W
– Q1 = 0 VAR
● Carga 2: la bomba de agua (inductiva)
Conocemos P y el cos φ. Necesitamos hallar Q.
1º) Hallamos el ángulo: φ2 = arccos (0,8) = 36,87°.
2º) Calculamos la reactiva: usamos la tangente.
Q2 = P2 · tan (36,87°) = 1.500 · 0,75 = 1.125 VAR
Resumen Carga 2:
– P2 = 1.500 W
– Q2 = 1.125 VAR
● Carga 3: la iluminación LED (inductiva)
Aquí conocemos la aparente (S) y el cos φ. La potencia aparente es S3 = 50 lámparas LED · 10 VA = 500 VA. Desglosamos S en sus catetos.
1º) Hallamos el ángulo: φ3 = arccos (0,9) = 25,84°
2º) Calculamos la activa:
P3 = S3 · cos (25,84°) = 500 · 0,9 = 450 W
3º) Calculamos la reactiva:
Q3 = S3 · sen (25,84°) = 500 · 0,436 = 218 VAR
Resumen Carga 3:
– P3 = 450 W
– Q3 = 218 VAR
Obtención de los Resultados Finales de la Instalación
Ahora unificamos los valores:
– Potencia activa total (PT):
PT = 2.000 + 1.500 + 450 = 3.950 W
– Potencia reactiva total (QT):
(como todas son inductivas, se suman. Si hubiera condensadores, restarían).
QT = 0 + 1.125 + 218 = 1.343 VAR
Con el triángulo total definido (PT y QT), calculamos los valores de la instalación.
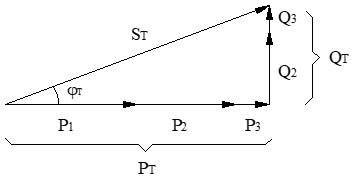
● Potencia aparente total (ST)
Aplicamos Pitágoras:
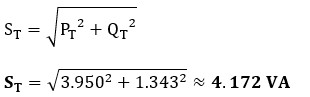
● Intensidad total (IT)
El dato que buscábamos para elegir el cable.
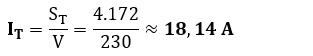
● Factor de Potencia total (cos φT)
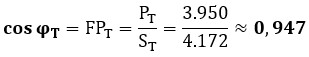
El ángulo de desfase total entre la tensión y la intensidad será:
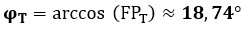
Conclusión del Ejercicio
Para terminar, comparemos nuestro resultado correcto con el error clásico de sumar las corrientes aritméticamente.
- Corriente radiador: 2.000W / 230V = 8,70 A
- Corriente bomba: 1.500W / (230V · 0,8) = 8,15 A
- Corriente LED: 500VA / 230V = 2,17 A
Suma aritmética (INCORRECTA): 8,70 + 8,15 + 2,17 = 19,02 A
Diferencia: el cálculo vectorial nos da 18,14 A, mientras que la suma simple da 19,02 A. Aunque en este ejemplo pequeño la diferencia es de casi 1 A, en instalaciones industriales grandes este error puede llevar a sobredimensionar transformadores y gastar miles de euros en cobre innecesario. Además, el cálculo vectorial nos ha permitido conocer el nuevo Factor de Potencia (0,95), un dato que la suma aritmética ignora por completo.
Conclusiones Generales de los Receptores Monofásicos en Paralelo
El estudio de los receptores monofásicos en paralelo mediante el triángulo de potencias nos deja 3 lecciones fundamentales para cualquier estudiante o profesional de la electricidad:
● La suma aritmética de intensidades es un error económico: si sumamos las corrientes de cada aparato directamente (I1 + I2...), obtendremos un valor (19,02 A) superior al real (18,14 A).
Aunque esto nos deja del lado de la seguridad, nos hará gastar dinero innecesariamente en cables más gruesos y protecciones sobredimensionadas.
● El cálculo por potencia activa es un error peligroso: el verdadero riesgo está en sumar solo los Vatios (W) y dividir por la tensión, ignorando la reactiva. En nuestro ejemplo, esto daría 3.950 W / 230 V = 17,17 A.
¡Cuidado! Estaríamos creyendo que circulan 17,17 A cuando en realidad circulan 18,14 A. Este error de subestimación es la causa de muchos disparos intempestivos de protecciones y calentamiento de líneas (podríamos instalar cables más finos de lo necesario, creando riesgo de incendio).
● La trigonometría es nuestra aliada: no hace falta dominar los números complejos para resolver circuitos profesionales. Con entender el teorema de Pitágoras y las funciones seno/coseno/tangente, podemos dimensionar instalaciones con total precisión.
Solo usando la potencia aparente (S), que combina vatios y reactiva, obtenemos el valor exacto para ajustar la instalación a la realidad física y normativa.
Resonancia Paralelo (Circuito Tanque)
Al igual que ocurre en el circuito serie, el circuito paralelo R-L-C presenta un comportamiento extraordinario bajo ciertas condiciones de frecuencia. Este fenómeno, a menudo denominado antirresonancia o efecto de "circuito tanque", es la base fundamental de los sintonizadores de radio y osciladores, pero también conlleva implicaciones críticas en la distribución de energía.
A diferencia del caso serie, aquí no buscamos facilitar el paso de la corriente, sino que ocurre un bloqueo selectivo donde la energía queda atrapada oscilando entre los componentes reactivos.
La Condición de Resonancia
La resonancia en paralelo ideal se produce cuando la componente reactiva de la corriente que baja por la rama de la bobina es igual y opuesta a la corriente que baja por la rama del condensador. Para que esto ocurra, sus reactancias deben igualarse:
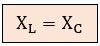
Existe una única frecuencia (fr) para cada circuito, donde XL y XC se igualan, ya que la primera aumenta y la segunda disminuye con la frecuencia.
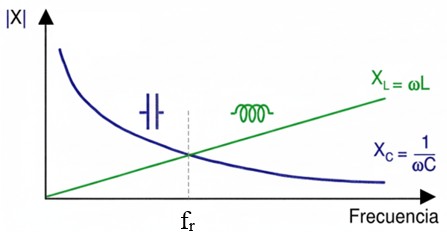
Dado que las corrientes en la bobina (IL) y en el condensador (IC) están desfasadas 180° entre sí (una se retrasa y la otra se adelanta respecto a la tensión), cuando sus valores óhmicos se igualan, sus efectos se cancelan mutuamente desde el punto de vista de la fuente de alimentación.
Impedancia Máxima e Intensidad Mínima
Cuando se alcanza la condición anterior, el comportamiento del circuito es diametralmente opuesto al de la resonancia en serie:
● Impedancia máxima: el conjunto paralelo opone su mayor resistencia posible al paso de la corriente. En un circuito ideal (sin resistencia interna), la impedancia (Z) tendería a infinito. En la realidad, la impedancia es muy alta y puramente resistiva (Z = L / (C · R)).
● Intensidad mínima: según la Ley de Ohm (I = V/Z), al ser la impedancia máxima, la corriente que la fuente necesita suministrar al circuito cae a su valor mínimo, apenas necesaria para compensar las pequeñas pérdidas por calor en los componentes.
Frecuencia de Resonancia
La frecuencia a la que ocurre este equilibrio singular es la misma que en el circuito serie (asumiendo una resistencia interna de la bobina despreciable frente a su reactancia). Igualamos las reactancias y despejamos:

Esto nos lleva nuevamente a la fórmula de Thomson, válida tanto para serie como para paralelo (con pérdidas resistivas muy bajas):
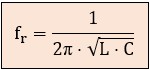
Peligro de Sobrecorrientes
Este es el aspecto más contraintuitivo y peligroso de la resonancia en paralelo. Aunque el amperímetro conectado a la salida de la fuente marque una corriente casi nula (ej. 0,1 A), dentro del bucle bobina-condensador la situación es muy diferente.
Se produce una amplificación de corriente (factor Q). La energía se transfiere cíclicamente del campo magnético de la bobina al campo eléctrico del condensador y viceversa.
Las corrientes individuales que circulan por la rama del condensador (IC) y la bobina (IL) pueden ser mucho mayores que la corriente total de línea.
Advertencia: Podríamos tener una línea alimentando con solo 1 Amperio, pero tener corrientes circulantes internas de 50 o 100 Amperios entre el condensador y la bobina. Si los conductores de interconexión o los propios componentes no están dimensionados para esta "corriente resonante", pueden fundirse o explotar, a pesar de que la protección general de la línea nunca salte.
Este problema aún puede agravarse si se produce el fenómeno de la resonancia paralela en presencia de armónicos de la red. Si la frecuencia natural del sistema (inductancia + condensadores) coincide con la de un armónico (ej. 250 Hz), las corrientes armónicas quedan atrapadas en un bucle, generando sobreintensidades capaces de destruir componentes esenciales de la instalación.
Aplicaciones de la Resonancia Paralelo
La propiedad única del circuito tanque paralelo, la de presentar una impedancia infinita (o máxima) a una frecuencia concreta, es la piedra angular de la transmisión de información inalámbrica. Sin este fenómeno, la radio y la TV tal como las conocemos no existirían.
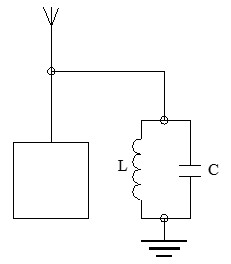
El circuito resonante en paralelo es el encargado de "elegir" qué queremos escuchar. El aire está lleno de miles de ondas de radio de diferentes frecuencias chocando contra la antena simultáneamente. ¿Cómo aislamos una sola?
Se conecta el circuito L-C paralelo asociado a la antena y tierra. El comportamiento es el inverso al caso serie:
– Para la frecuencia de resonancia (fr): la impedancia del circuito se vuelve extremadamente alta (teóricamente infinita). Esto provoca que la corriente de esa frecuencia específica no pueda derivarse a tierra y genere una caída de tensión máxima en los extremos del circuito. Esta tensión es la que capturamos y amplificamos: es la emisora que escuchamos.
– Para el resto de frecuencias: la impedancia del circuito es muy baja. Todas las demás señales de radio (otras emisoras o ruido) encuentran un camino fácil hacia tierra a través de la bobina (frecuencias bajas) o el condensador (frecuencias altas), siendo cortocircuitadas y eliminadas antes de entrar al amplificador.
Además de filtrar, el circuito paralelo es capaz de almacenar energía oscilando entre el campo magnético y el eléctrico. Esto permite usarlo en osciladores, circuitos encargados de generar frecuencias patrón estables, imprescindibles en relojes digitales, transmisores y ordenadores.
También te puede interesar:

Condensador Eléctrico (Capacitor): Qué es, Tipos, Código y Fórmulas
Bobina o Inductor Eléctrico: Qué es, Símbolo y Funcionamiento (Ley de Lenz)
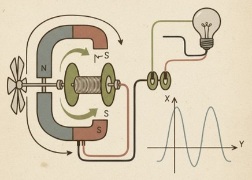
Generación de Corriente Alterna: El Alternador y la Inducción Electromagnética
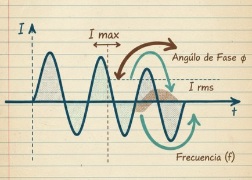
Parámetros de la Onda Senoidal (CA): Frecuencia, Periodo y Valor Eficaz (RMS)
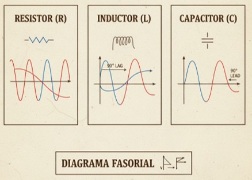
Receptores en Corriente Alterna: Circuitos R, L y C (Resistivo, Inductivo y Capacitivo)
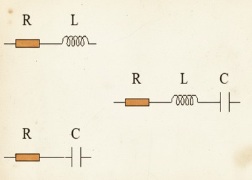
Circuitos Serie RL, RC y RLC: Impedancia, Fórmulas y Resonancia
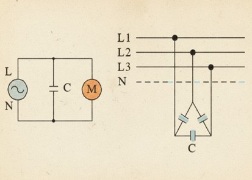
Factor de Potencia (cos φ) y Energía Reactiva: Qué es y Cómo Corregirlo
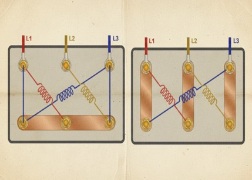
Conexión Estrella y Triángulo: Diferencias, Esquemas y Voltajes (230/400V)