
Resistencias en Paralelo: Fórmula, Resistencia Equivalente y Ventajas
A diferencia del circuito en serie (donde la corriente solo tiene un camino), conectar resistencias en paralelo es como abrir varios carriles en una autopista. La corriente eléctrica se divide entre las distintas ramas, permitiendo que cada componente funcione de forma independiente con el mismo voltaje.
Esta configuración tiene una propiedad matemática curiosa pero vital: la Resistencia Equivalente (Req) siempre será menor que la resistencia más pequeña del circuito.
En esta guía aprenderás la fórmula general, el truco del 'producto sobre suma' y cómo se aplica el principio del Divisor de Corriente.
🔌 Circuito en Paralelo: Resumen Rápido
Voltaje (V): Vt = V1 = V2 = ...
Corriente (I): It = I1 + I2 + ...
1
RT
1
R1
1
R2
1
R3
🗝️ Truco para solo 2 resistencias:
RT =
R1 · R2
R1 + R2
🚀 Atajo para n resistencias iguales:
RT =
R
n
R: valor de la resistencia | n: cantidad de resistencias.
💡 Recuerda: El voltaje es igual en cada componente.
Técnicamente, una resistencia es un componente cuyo propósito es ofrecer una oposición controlada al paso de la corriente eléctrica (I). Gracias a esta propiedad, permite gestionar el flujo de electrones en un circuito y crear caídas de tensión específicas entre sus terminales. Se mide en ohmios (Ω).
Esta configuración es la base de casi todas las instalaciones eléctricas que utilizamos diariamente. Es el patrón detrás del flujo de electricidad tanto en un dispositivo básico como en los enchufes de cualquier instalación.
A continuación, se procederá al análisis de las fórmulas para calcular la resistencia equivalente de los circuitos en paralelo. Sin embargo, para ahorrar tiempo, se puede hacer uso de esta calculadora de resistencias en paralelo que hace el cálculo al instante.
Contenidos
- Características: Mismo Voltaje, Distinta Corriente
- Fórmulas de Cálculo de la Resistencia Equivalente o Total
- Ley de Ohm Aplicada a Circuitos con Resistencias en Paralelo
- Ejercicios Resueltos con Resistencias en Paralelo
- Potencia Eléctrica en Paralelo
- Aplicación Práctica: El Divisor de Corriente
- ¿Por qué se Usa en las Casas? (Independencia)
Características: Mismo Voltaje, Distinta Corriente
El circuito en paralelo es el pilar de la distribución de energía y, por ende, de cualquier instalación eléctrica actual. Su diseño único dicta cómo se comportan las magnitudes eléctricas principales: la corriente eléctrica (I) y la tensión (V).
Los Nudos Eléctricos
Un circuito se considera en paralelo cuando sus componentes (en este caso, resistencias) están conectados entre 2 puntos o nudos comunes.
Si imaginamos un circuito con varias resistencias (R1, R2, R3), el terminal inicial de R1, R2 y R3 está conectado en un punto (Nudo A), y el terminal final de las tres está conectado en otro punto diferente (Nudo B).
Esta configuración obliga a la corriente total (IT) que sale de la fuente a dividirse en el nudo A, fluyendo a través de cada resistencia por separado. El nudo B es donde estas corrientes se suman de nuevo para formar de nuevo la corriente total. Por lo tanto, el sistema ofrece múltiples caminos independientes para que la electricidad circule.
Esta independencia de caminos es la que otorga al circuito en paralelo su principal ventaja: si la ruta que pasa por R2 se abre (por ejemplo, la resistencia se quema), la corriente puede seguir fluyendo sin interrupción a través de las ramas de R1 y R3.

Voltaje Constante (VT = V1 = V2)
En un circuito en paralelo, el principio más fundamental es la uniformidad del voltaje. La tensión eléctrica, la fuerza que impulsa a los electrones, es idéntica a través de cada rama y a través de la fuente de alimentación.

donde:
VT es la tensión total de la fuente
V1, V2, V3, … son las tensiones medidas en cada resistencia individual (R1, R2, R3, …).
Dado que todos los componentes están conectados directamente entre los mismos 2 puntos de diferente potencial, los nudos A y B, la diferencia de potencial (voltaje) entre esos 2 puntos es la misma para todos. No hay división de energía potencial a lo largo del camino, como ocurre en los circuitos en serie.
Analogía del agua: imaginemos una tubería principal (la fuente de tensión) que se divide en varias tuberías más pequeñas (las ramas con resistencias) antes de volver a unirse. La presión del agua (el voltaje) en la entrada de cada tubería pequeña será exactamente la misma que la presión en la tubería principal. No importa si una rama es más estrecha (mayor resistencia) o más ancha (menor resistencia); la presión que empuja al agua sigue siendo la misma.

Esta es la razón por la cual las instalaciones domésticas se realizan en paralelo: todos los aparatos (lámparas, televisores, neveras) necesitan recibir la tensión estándar de la red (por ejemplo, 230V en Europa o 120V en América) para funcionar correctamente.
Corriente Dividida (Kirchhoff)
Mientras que la tensión se mantiene constante, la corriente se comporta de manera opuesta: se divide.
La corriente total (IT) que sale de la fuente viaja hasta el nudo A y luego se divide para fluir por cada rama en proporción inversa a la resistencia de esa rama. Cuanto menor sea la resistencia de una rama, mayor será la porción de corriente que fluirá a través de ella, ya que, según la Ley de Ohm, la intensidad es I = V / R.
La Ley de Corrientes de Kirchhoff (LCK) establece que la suma de las corrientes que entran en un nudo debe ser igual a la suma de las corrientes que salen. Aplicado al circuito total, esto significa:

donde:
IT es la corriente suministrada por la fuente.
I1, I2, I3, … son las corrientes que pasan a través de cada resistencia individual (R1, R2, R3, …).
La corriente total IT es simplemente la suma de las demandas individuales de corriente de cada componente.
Por ejemplo, si se conectan 3 lámparas en paralelo, la corriente total IT consumida por el circuito es igual a la suma de la corriente que necesita la lámpara 1, más la que necesita la lámpara 2, más la que necesita la lámpara 3. Esta es la razón por la que al añadir más aparatos a un enchufe, la corriente total que viene del panel eléctrico aumenta.

Fórmulas de Cálculo de la Resistencia Equivalente o Total
Para trabajar y diseñar circuitos eléctricos en paralelo, es indispensable manejar las fórmulas que rigen la corriente, la tensión y, fundamentalmente, la resistencia total o equivalente del sistema
Para poder utilizar la Ley de Ohm y calcular la corriente total que circula por el circuito, primero es necesario representar el conjunto de resistencias mediante un único valor. Este valor unificado, conocido como resistencia equivalente (Req) o resistencia total (RT), condensa el efecto combinado de todas y cada una de las resistencias individuales.
Concepto de Circuito Equivalente
Un circuito equivalente es una versión simplificada diseñada para replicar fielmente el comportamiento externo del circuito original.
Su propósito es reemplazar múltiples componentes (en este caso, resistencias) por uno solo que, desde sus terminales, presente idénticas características de voltaje y corriente. Al conectar la misma fuente de alimentación, esta no puede distinguir entre el circuito de múltiples componentes y su equivalente simplificado.
Por tanto, el circuito queda simplificado a una sola resistencia hipotética que podría sustituir a todas las resistencias conectadas en paralelo permitiendo que la fuente de alimentación suministre exactamente la misma cantidad de corriente al circuito.


Fórmula General (3 o más)
El objetivo de calcular la resistencia equivalente Req o total RT es determinar una única resistencia que, colocada en el circuito, consumiría la misma corriente total y mantendría la misma tensión que todo el conjunto de resistencias conectadas en paralelo.
A diferencia de los circuitos en serie (donde las resistencias simplemente se suman), en paralelo la resistencia equivalente se calcula sumando los recíprocos (inversos) de las resistencias individuales.
La fórmula general para cualquier número de resistencias conectadas en paralelo es:

donde:
RT es la resistencia equivalente o total, medida en ohmios (Ω).
R1, R2, R3, … son los valores óhmicos de cada resistencia conectada en paralelo.

Para obtener el valor final de RT, es necesario calcular el recíproco del resultado de la suma:

Un aspecto fundamental de los circuitos en paralelo es que añadir más ramas disminuye la resistencia total del sistema.
La resistencia total (RT) siempre será menor que la resistencia individual más pequeña presente en el circuito.
Esto ocurre porque cada resistencia adicional abre un nuevo camino para el flujo de electrones. Al ofrecer más opciones de flujo, el circuito en su conjunto se "opone menos" al paso de la corriente, reduciendo su resistencia general.
El Truco Rápido (Solo 2)
Cuando el circuito solo consta de 2 resistencias (R1 y R2) conectadas en paralelo, existe una simplificación algebraica muy útil conocida como la fórmula del "producto sobre la suma":
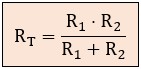
Resistencias Iguales: R / n
Si tenemos n resistencias, todas con el mismo valor (R), el cálculo es aún más sencillo. Simplemente se divide el valor de una resistencia por el número total de resistencias:

Por ejemplo, 4 resistencias de 10 Ω en paralelo resultan en una resistencia equivalente de 10 Ω / 4 = 2,5 Ω.
Conductancia de un Circuito con Resistencias en Paralelo
En el análisis de circuitos, a veces es más conveniente trabajar con el concepto de conductancia (G), que es la medida de cuán fácilmente un componente permite el paso de la corriente. La conductancia es simplemente la inversa de la resistencia:

La unidad de medida de la conductancia es el Siemens (S).
El uso de la conductancia simplifica la fórmula de resistencia en paralelo, ya que la conductancia equivalente (GT) de un circuito en paralelo es la suma simple de las conductancias individuales:

Una vez que se calcula GT, la resistencia equivalente RT se obtiene invirtiendo el resultado: RT = 1/GT. Esta es la manera más conceptual de entender por qué la fórmula general de RT involucra recíprocos.
Ley de Ohm Aplicada a Circuitos con Resistencias en Paralelo
La Ley de Ohm es la relación fundamental que vincula la tensión (V), la corriente (I) y la resistencia (R) en cualquier circuito eléctrico. En su forma más conocida, se expresa como V = R · I.

Esta ley se puede aplicar de 2 maneras en un circuito en paralelo:
– A todo el circuito (usando VT, IT, RT).
– A cada componente individual (usando Vn, In, Rn).
Corriente Total del Circuito
La corriente total (IT) es la cantidad de corriente que sale de la fuente de tensión (VT) y que debe ser repartida entre todas las ramas del circuito. El paso clave es usar la resistencia total RT.

Para calcular esta corriente IT, utilizamos la Ley de Ohm, sustituyendo la resistencia individual (R) por la resistencia total o equivalente (RT) del circuito.

donde:
IT es la corriente total (en Amperios, A).
VT es la tensión total suministrada por la fuente (en Voltios, V).
RT es la resistencia equivalente de todo el circuito paralelo (en Ohmios, Ω).
Esta fórmula nos permite ver que, dado que RT siempre es un valor menor que la resistencia individual más pequeña, la corriente total (IT) será mayor que la corriente que fluiría si solo estuviera conectada esa resistencia más pequeña.
Esto tiene sentido, ya que al añadir más caminos en paralelo, estamos facilitando el flujo eléctrico, y la fuente debe suministrar más corriente para satisfacer la demanda de todas las ramas.
Corrientes Individuales de cada Resistencia
Una vez que se conoce la tensión total de la fuente (VT) y el valor de cada resistencia individual (Rn), la corriente que fluye a través de cada rama (In) se calcula directamente mediante la Ley de Ohm.
Recordando que en paralelo la tensión es constante e igual en todas las ramas (Vn = VT), las corrientes individuales se obtendrían de la siguiente manera:
– Corriente en R1:

– Corriente en R2:

– Y así sucesivamente para cada resistencia Rn:


Tensión Total de un Circuito con Resistencias en Paralelo
En ocasiones, al analizar un circuito, se conoce la resistencia equivalente total (RT) y la corriente total (IT), pero se desconoce la tensión que se está aplicando (tensión de la fuente). Al utilizar la Ley de Ohm con los valores totales, podemos determinar la tensión del circuito.
La fórmula de la tensión total será:

donde:
VT es la tensión total (en Voltios, V).
IT es la corriente total que circula por el circuito (en Amperios, A).
RT es la resistencia equivalente del circuito (en Ohmios, Ω).
Si ahora aplicamos esta misma fórmula a cualquier rama individual (Vn = Rn · In), la tensión debe ser idéntica a la tensión total calculada (VT = RT · IT). Este es un excelente método de verificación para asegurar que todos los cálculos intermedios son correctos.
Ejercicios Resueltos con Resistencias en Paralelo
A continuación, se muestran 3 ejercicios resueltos de resistencias en paralelo sobre el cálculo de la corriente total que sale de la fuente, el cálculo de corrientes individuales y el Cálculo de la tensión total de la fuente.
Corriente Total que Sale de la Fuente
Un circuito en paralelo está conectado a una fuente de 12 Voltios (VT). El circuito contiene dos resistencias: R1 = 4 Ω y R2 = 6 Ω. Calcular la resistencia total y obtener la corriente total IT.
Utilizaremos la fórmula simplificada para 2 resistencias (producto sobre la suma):

La resistencia equivalente del circuito es 2,4 Ω. (Nota: es menor que la resistencia más pequeña, 4 Ω, como debe ser en paralelo).
Para calcular la corriente total (IT) usamos la Ley de Ohm:



Corrientes Individuales
Un circuito con 3 resistencias (R1 = 10 Ω, R2 = 5 Ω, y R3 = 2 Ω) está conectado en paralelo a una fuente de 20 Voltios (VT). Calcular la corriente individual que pasa por cada resistencia (I1, I2, I3). Verificar el resultado calculando la corriente total (IT).
– Corriente individuales: en paralelo, la tensión es la misma en todas las ramas: V1 = V2 = V3 = VT = 20 V. Aplicamos la Ley de Ohm a cada rama.

Se observa que la resistencia más baja, R3 = 2 Ω, consume la mayor corriente, 10 A.
– Verificación LCK: Según la Ley de Corrientes de Kirchhoff (LCK), la corriente total es la suma de las corrientes de las ramas.



– Verificación opcional (cálculo de RT): para verificar si el resultado es correcto, podemos calcular RT y luego IT usando la Ley de Ohm total (IT = VT /RT) al circuito equivalente.


Tensión Total de la Fuente
Un circuito con 3 resistencias en paralelo R1 = 20 Ω, R2 = 30 Ω y R3 = 60 Ω consume una corriente total IT de 9 A. Calcular la resistencia equivalente (RT) y la tensión total (VT).
Usamos la fórmula general de los recíprocos para las 3 resistencias:

Para obtener la tensión total usamos la Ley de Ohm en el circuito equivalente:



Para confirmar que la tensión de 90 V es correcta, vamos a calcular las corrientes individuales (I1, I2, I3), verificar la LCK (IT = I1 + I2 + I3) y usar la Ley de Ohm en una rama (Vn = In · Rn) para asegurar que el voltaje es 90 V.

Tomamos la rama 2 como ejemplo, con I2 = 3 A y R2 = 30 Ω:

Potencia Eléctrica en Paralelo
La potencia eléctrica (P) representa la velocidad a la que la energía eléctrica es consumida o disipada por un componente, típicamente en forma de calor y/o luz. Se mide en Vatios (Watts, W) y es un parámetro fundamental para el diseño de circuitos, ya que determina la capacidad de carga de los componentes y de la fuente de alimentación.
Potencia Disipada Individual de cada Resistencia
En un circuito en paralelo, la potencia disipada por cada resistencia es independiente de las otras, pero utiliza la tensión total de la fuente (VT) y la corriente individual (In) que fluye a través de esa rama.
La potencia en cualquier componente de corriente continua (CC) se define por la fórmula general P = V · I. Al aplicar esto a una rama (n) en un circuito paralelo, donde Vn = VT, obtenemos:

Además, gracias a la Ley de Ohm, podemos expresar la potencia de otras 2 maneras equivalentes, lo que resulta muy útil dependiendo de qué valores del circuito conozcamos:


La fórmula de la potencia en función de la tensión y la resistencia es especialmente relevante en paralelo. Dado que VT es constante, revela que cuanto menor sea la resistencia (Rn), mayor será la potencia consumida por esa rama.
Por ejemplo, una bombilla de baja resistencia (que consume mucha potencia) brillará más que una de alta resistencia si ambas están conectadas al mismo voltaje en paralelo.
Potencia Disipada Total del Circuito
La potencia total (PT) del circuito en paralelo es la cantidad total de energía que la fuente de alimentación debe suministrar para operar todas las resistencias.
El principio de conservación de la energía nos dice que la potencia total suministrada por la fuente debe ser igual a la potencia total consumida por todas las cargas.
Por lo tanto, en cualquier circuito, incluyendo el paralelo, la potencia total es la suma de las potencias disipadas por cada componente:

Un método para verificar la corrección de los cálculos de potencia individuales consiste en determinar la potencia total mediante una segunda vía, aplicando los valores de tensión total y corriente total del circuito equivalente.


Alternativamente, si conocemos la resistencia equivalente RT, también podemos usar las otras formas de la ley de potencia:


La suma de las potencias individuales siempre será igual a la potencia calculada con los valores totales. Si estos valores no coinciden, es una señal de que hay un error en el cálculo de RT o de las corrientes individuales.
Ejercicio Resuelto de las Potencias de Cada Resistencia y Resistencia Total
Un circuito con las siguientes resistencias R1 = 60 Ω, R2 = 40 Ω y R3 = 24 Ω, está conectado en paralelo a una fuente de 120 Voltios (VT). Calcular las potencias de cada resistencia y la potencia total, verificando con el circuito equivalente.
Primero aplicamos la Ley de Ohm a cada rama para obtener las corrientes individuales:

– Potencias individuales:

Se observa que la resistencia más baja, R3, consume la mayor potencia.
– Suma de potencias:



– Verificación con el circuito equivalente: usar el circuito equivalente requiere calcular primero la corriente total (IT).

Aplicación Práctica: El Divisor de Corriente
Un divisor de corriente es un circuito eléctrico que distribuye la corriente total proveniente de una fuente entre dos o más ramas en paralelo, siguiendo la ley de corrientes de Kirchhoff y la relación inversa con la resistencia de cada rama.
El principio fundamental es intuitivo: la corriente eléctrica es "perezosa". Siempre preferirá circular en mayor cantidad por el camino que le ofrezca menos oposición (menor resistencia). Por tanto, la corriente se reparte de forma inversamente proporcional al valor de cada resistor.
El "Truco" para Dos Ramas en Paralelo
Este es el caso más común en diseños rápidos. Si tenemos una corriente total (IT) que entra en un nudo con 2 resistores (R1 y R2), se puede calcular la corriente de una rama usando el valor de la otra.
Para hallar la corriente en el resistor 1 (I1):
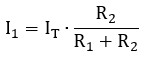
Para hallar la corriente en el resistor 2 (I2):
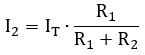
🔍 Fíjate en el numerador: para calcular la corriente que pasa por una rama, en el numerador de la fracción debes poner el valor del resistor de la rama opuesta. Cuanto más grande sea el resistor de enfrente, más corriente "empujará" hacia el camino que estás calculando.
Ejemplo: Vamos a calcular corrientes sin calcular voltajes. De la fuente de un circuito con 2 resistores en paralelo, R1 = 2 Ω y R2 = 8 Ω, salen 10 Amperios. ¿Cuánta corriente pasa por el resistor R2 de 8 Ω?
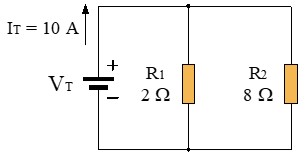
Aplicamos la fórmula para calcular la corriente I2 (teniendo en cuenta R1):
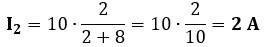
Sin necesidad de saber el voltaje de la batería ni la resistencia total, sabemos que por la rama de mayor resistencia (8 Ω) solo pasan 2 Amperios, mientras que por la de menor resistencia (2 Ω) pasan los 8 Amperios restantes.
Caso General (Más de Dos Ramas en Paralelo)
Si tenemos 3 o más ramas, el "truco" de la rama opuesta no funciona directamente. En este caso, la regla se basa en la conductancia (G), que es la inversa de la resistencia (G = 1/R).
La fórmula general es:
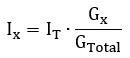
O expresado con resistencias para que sea más fácil de aplicar si ya tenemos la RT del paralelo:
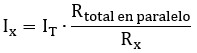
Ejemplo: En el siguiente circuito, la corriente total de la fuente es de 16 A y dispone de 3 resistores en paralelo con los siguientes valores: R1 = 10 Ω, R2 = 5 Ω y R3 = 2 Ω. ¿Qué corriente pasa por cada resistor?
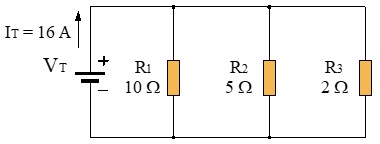
Obtenemos la resistencia total o equivalente:
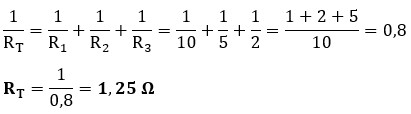
Los valores de cada resistencia se obtienen con la fórmula general:

¿Por qué se Usa en las Casas? (Independencia)
El comportamiento único de la tensión y la corriente en un circuito paralelo ofrece 3 ventajas primordiales sobre los circuitos en serie:
● Tolerancia a fallos e independencia operacional (fiabilidad): la principal ventaja del paralelo es la independencia de sus ramas. Si una resistencia o carga se daña, se desconecta o se "abre" (lo que detiene el flujo de corriente en esa rama específica), el resto de las ramas permanecen conectadas a la fuente de tensión y siguen funcionando con normalidad.
Por ejemplo,actualmente las luces siempre se cablean en paralelo. Así, si una lámpara falla, las demás siguen funcionando.

● Tensión uniforme y nominal (requisito de carga): en paralelo todos los componentes reciben la misma tensión de la fuente (VT). Los aparatos eléctricos (lámparas, televisores o electrodomésticos) están diseñados para operar a una tensión nominal específica (por ejemplo, 230V o 120 V).
Conectar estos aparatos en paralelo garantiza que cada uno reciba exactamente la tensión que necesita, sin que el voltaje se "divida" o se reduzca al añadir más dispositivos.

● Flexibilidad para añadir carga y reducción de resistencia: al añadir una nueva carga (otra resistencia o aparato) en paralelo, lo que ocurre es que se abre un camino adicional para el flujo de corriente. Esto, como hemos visto, disminuye la resistencia equivalente (RT) total del circuito.

Las cargas ya conectadas no se ven afectadas en su funcionamiento. Su tensión (V) permanece constante y su corriente (I) individual no cambia. La única magnitud que aumenta es la corriente total (IT) que la fuente debe suministrar. Esto permite que los circuitos crezcan y se adapten a la demanda sin comprometer el rendimiento de los dispositivos ya conectados.
También te puede interesar:

Carga Eléctrica (Q): Qué es, Tipos y Ley de Coulomb

Voltaje o Tensión Eléctrica: ¿Qué es la Diferencia de Potencial?

Corriente Eléctrica o Intensidad (I): Qué es, Tipos y Efecto Joule

Resistencia Eléctrica (R) y Resistividad: Qué es, Símbolo y Tipos

Ley de Ohm: Fórmula, Triángulo y Ejemplos Resueltos (V = I · R)

Potencia Eléctrica (P) y Ley de Watt: Fórmulas, Triángulo y Tipos

Energía Eléctrica (E): Qué es, Fórmula (kWh) y Diferencia con Potencia

Resistencias en Serie: Fórmula, Circuito Equivalente y Divisor de Tensión

Circuitos Mixtos (Serie-Paralelo): Cómo Resolverlos Paso a Paso

Multímetro Digital (Polímetro): Qué es, Partes y Cómo Usarlo

