Resistencias en Serie

Un circuito de resistencias en serie es aquel en el que los componentes se conectan sucesivamente, formando una única trayectoria para la corriente eléctrica, similar a los eslabones de una cadena o los vagones de un tren.

Lo más importante de esta configuración es que la corriente eléctrica solo tiene un único camino para circular. La salida (terminal) de la primera resistencia se conecta directamente a la entrada de la segunda, y así sucesivamente.

Recordamos que una resistencia es un componente electrónico diseñado para oponerse al flujo de la corriente eléctrica (I). Su función principal es controlar el flujo de corriente y establecer caídas de tensión dentro de un circuito. Se mide en ohmios (Ω).

Esta configuración es fundamental en electricidad y electrónica, ya que permite resolver numerosos problemas prácticos relacionados con la distribución de voltaje y el control de la corriente. Comprender su comportamiento sirve de base para analizar circuitos más complejos.

Principios del Circuito con Resistencias en Serie

Para analizar y calcular con precisión cualquier circuito en serie, es indispensable comprender cómo se comportan las 2 magnitudes eléctricas principales: la corriente eléctrica (I) y la tensión (V).

La Corriente Eléctrica en un Circuito de Resistencias en Serie

El principio más importante y definitorio de una conexión en serie es la corriente. Dado que un circuito en serie ofrece un único camino para que los electrones fluyan desde el polo negativo al positivo de la fuente, la cantidad de carga que atraviesa cualquier punto es siempre la misma.

Analogía del agua: imaginemos la corriente eléctrica como el flujo de agua en una tubería. Si la tubería no tiene bifurcaciones (camino único), la cantidad de agua que pasa por un punto A, debe ser exactamente la misma que pasa por un punto B, sin importar las obstrucciones (resistencias) que se encuentren en el camino. Las resistencias limitan la magnitud de la corriente total, pero no la dividen.

Esto significa que si se mide la corriente en la primera resistencia, en la segunda, y así sucesivamente hasta la última resistencia, el valor será idéntico.

donde:

I_T ​es la corriente suministrada por la fuente.

I₁, I₂, I₃, … son las corrientes que pasan a través de cada resistencia individual (R₁, R₂, R₃, …).

El Voltaje en un Circuito de Resistencias en Serie

La tensión o diferencia de potencial total suministrada por la fuente representa la energía potencial disponible para mover la carga eléctrica. A medida que la corriente atraviesa cada resistencia consume parte de esa energía potencial, convirtiéndola generalmente en calor.

Este consumo de energía se manifiesta como una caída de tensión (V) a través de cada resistencia. Es decir, el voltaje no es el mismo a través de R₁ que a través de R₂ (a menos que ambas resistencias sean iguales).

Analogía del agua: si la corriente es el caudal de agua, la tensión es la presión. Una bomba (fuente de tensión) genera una presión total. Cuando el agua pasa por una obstrucción (resistencia), parte de esa presión se "gasta" para superarla, provocando una caída de presión a lo largo del camino.

La suma de todas las caídas de tensión individuales debe ser igual a la tensión total suministrada por la fuente. Este principio es conocido formalmente como la Ley de Tensión de Kirchhoff.

La Ley de Voltajes de Kirchhoff (LVK) dice que la suma algebraica de las caídas y elevaciones de tensión alrededor de cualquier trayectoria cerrada (malla) en un circuito es igual a cero. En la práctica, esto significa que la tensión de la fuente debe ser consumida totalmente por los componentes del circuito.

La fórmula de la tensión total es:

donde:

V_T es la tensión suministrada por la fuente (el voltaje total que entra al circuito).

V₁, V₂, V₃, … son las caídas de tensión medidas a través de cada resistencia individual (R₁, R₂, R₃, …).

La correcta aplicación de estos 2 principios (corriente constante y tensión repartida) es lo que permite utilizar la Ley de Ohm para calcular las propiedades de cada componente y del circuito en su totalidad.

Resistencia Equivalente o Total de un Circuito Serie

Para poder aplicar la Ley de Ohm al circuito en su conjunto y determinar la corriente total, necesitamos condensar el efecto de todas las resistencias individuales en un único valor. Este valor se conoce como la resistencia equivalente o resistencia total (R_T).

Concepto de Circuito Equivalente

El objetivo del circuito equivalente es reemplazar múltiples componentes (en este caso, resistencias) por un único componente que, desde el punto de vista de sus terminales externos, se comporte exactamente igual que el circuito original.

Un circuito equivalente es una versión simplificada de un circuito que, cuando se conecta a la misma fuente de alimentación, resulta en la misma corriente total y el mismo voltaje en los terminales que el circuito original.

El circuito se simplifica a una sola resistencia hipotética que podría sustituir a todas las resistencias conectadas en serie y, aun así, permitiría que la fuente de alimentación suministre exactamente la misma cantidad de corriente al circuito.

Desde la perspectiva de la fuente de tensión (por ejemplo, una batería), el circuito en serie actúa como si fuera una única resistencia grande. La fuente solo "ve" una oposición total al flujo de corriente, que es la suma combinada de todas las oposiciones individuales.

En una conexión en serie, al conectar una resistencia tras otra, estamos esencialmente alargando el camino que la corriente debe recorrer y añadiendo más obstáculos en su única ruta.

– Si cada resistencia se opone al flujo de corriente, al ponerlas en fila, cada una de ellas contribuye a la oposición total.

– En contraste con los circuitos en paralelo (donde se ofrecen caminos alternativos), el circuito en serie no ofrece rutas de escape; por lo tanto, la oposición total al paso de los electrones debe ser, por necesidad, mayor que la resistencia de cualquier componente individual.

– Por esta razón, la R_T de un circuito en serie siempre será mayor que la resistencia individual más grande presente en la conexión.

Resistencia Equivalente de un Circuito con Resistencias en Serie

Debido a que cada resistencia en serie actúa simplemente como una adición lineal de oposición al flujo, el cálculo de la resistencia total es sorprendentemente sencillo y directo. La resistencia total R_T es la suma de las resistencias individuales.

donde:

R_T es la resistencia equivalente o total, medida en ohmios (Ω).

R₁, R₂, R₃, … son los valores óhmicos de cada resistencia conectada en serie.

Si en el circuito se utilizan n resistencias que tienen el mismo valor (R), el cálculo se simplifica aún más, convirtiéndose en una multiplicación.

donde:

n es el número total de resistencias conectadas.

R es el valor óhmico de una sola resistencia.

Ejemplos de Cálculo de la Resistencia Equivalente

La aplicación de esta fórmula es fundamental y se ilustra mejor con ejemplos concretos.

Ejemplo: Cálculo de R_T con resistencias de diferente valor

Suponemos que tenemos un circuito alimentado por una fuente de 12 V con 3 resistencias conectadas en serie: R1 = 10 Ω, R2 = 20 Ω y R3 = 30 Ω. Calcular la resistencia total equivalente y la corriente total de la fuente.

Para encontrar la resistencia total (R_T), simplemente sumamos sus valores:

Una vez que conocemos R_T, podemos usar la Ley de Ohm para calcular la corriente total (I_T) que sale de la fuente:

Ejemplo: Caso especial de resistencias iguales

Tenemos 3 resistencias idénticas conectadas en serie, y cada una tiene un valor de 100 Ω. Calcular la resistencia total.

Este concepto de la resistencia equivalente es el primer paso fundamental para el análisis completo del circuito, ya que la corriente total que hemos calculado (I_T) es la misma que fluye a través de cada resistencia individual.

Ley de Ohm Aplicada a Circuitos con Resistencias en Serie

La Ley de Ohm es la relación fundamental entre la tensión (V), la corriente (I) y la resistencia (R). Aplicada estratégicamente a un circuito en serie, nos permite conocer el comportamiento eléctrico de todo el sistema y de cada uno de sus componentes individuales.

Esta ley se puede aplicar de 2 maneras en un circuito en serie:

– A todo el circuito (usando V_T, I_T, R_T).

– A cada componente individual (usando V_n, I_n, R_n).

Corriente Total de un Circuito con Resistencias en Serie

El primer cálculo que debemos realizar es el de la corriente total que sale de la fuente de alimentación. Para esto, usamos el circuito equivalente y tratamos al circuito serie como si fuera una sola resistencia equivalente. El paso clave es usar la resistencia total R_T.

Para calcular la corriente total (I_T), aplicamos la Ley de Ohm utilizando el voltaje total de la fuente (V_T) y la resistencia total que calculamos previamente (R_T).

Dado el principio fundamental de los circuitos serie (I_T = I₁ = I₂ = I₃ = …), esta corriente I_T calculada es la única corriente que pasa a través de todas y cada una de las resistencias individuales. Este valor es el motor de los siguientes cálculos.

Caídas de Tensión Individuales de cada Resistencia en Serie

Una vez que conocemos la corriente total (I_T), podemos determinar la cantidad de voltaje que es consumida o "cae" a través de cada resistencia individual.

Recordemos que, aunque la corriente es la misma, cada resistencia se opone al flujo de manera diferente, consumiendo una porción distinta de la energía potencial total (voltaje).

Para calcular la caída de tensión (V_n) a través de cualquier resistencia (R_n), aplicamos la Ley de Ohm solo a esa resistencia, usando su valor y la corriente total que pasa a través de ella.

– Caída de tensión en R₁:

– Caída de tensión en R₂:

– Y así sucesivamente para cada resistencia Rn:

Como paso final, debemos verificar que la suma de todas las caídas de tensión individuales es igual a la tensión total suministrada por la fuente. Este paso confirma la exactitud de nuestros cálculos y demuestra el cumplimiento de la Ley de Voltajes de Kirchhoff (LVK):

Ejemplo: Caídas de tensión de cada resistencia

 Si V_T = 12 V, R_T = 60 Ω, e I_T = 0,2 A, y las resistencias eran R₁ = 10 Ω, R₂ = 20 Ω, R₃ = 30 Ω. Calcular las caídas de tensión en cada resistencia y comprobar el valor de la tensión total V_T.

– Caídas de tensión:

– Verificación LVK:

Como 12 V = V_T, los cálculos son correctos.

Este procedimiento sistemático, calcular primero la resistencia total (R_T), luego la corriente total (I_T), y finalmente los voltajes individuales (V_n), constituye la metodología más sólida y confiable para analizar cualquier circuito de resistencias en serie.

Potencia Eléctrica en Circuitos con Resistencias en Serie

La potencia eléctrica (P), medida en vatios (W), representa la velocidad a la que la energía eléctrica es consumida o disipada por los componentes del circuito. En el caso de las resistencias, esta energía se disipa principalmente en forma de calor (efecto Joule).

Comprender la potencia es de vital importancia, no solo por el consumo energético, sino también para la selección correcta de componentes, asegurando que una resistencia pueda soportar el calor generado sin quemarse.

Potencia Disipada Individual de cada Resistencia en Serie

Cada resistencia en el circuito serie consume una porción de la potencia total suministrada por la fuente. El cálculo de esta potencia individual (P_n​) se realiza aplicando las diversas formas de la Ley de Ohm combinada con la fórmula fundamental de potencia.

Dado que en un circuito serie conocemos la corriente (I_T​) y la caída de tensión (V_n​) en cada resistencia (R_n​), disponemos de 3 fórmulas equivalentes para calcular la potencia disipada por la resistencia R_n​:

● Usando tensión y corriente: esta es la fórmula fundamental. Multiplica la caída de tensión a través de la resistencia por la corriente que pasa por ella, siendo I_n = I_T.

● Usando corriente y resistencia: al ser I_n = I_T, esta es a menudo la forma más común de cálculo, ya que la corriente total se determina al inicio.

● Usando tensión y resistencia: útil cuando ya se ha calculado la caída de tensión en el componente.

Al calcular P_n​, se deben seleccionar resistencias con una potencia superior a la potencia calculada. Por ejemplo, si una resistencia disipa 0,8 W, se debe usar una resistencia estándar de 1 W o más, para garantizar un funcionamiento seguro y estable.

Potencia Disipada Total del Circuito con Resistencias en Serie

De acuerdo con el principio de conservación de la energía, la potencia total que la fuente suministra al circuito debe ser igual a la suma de toda la potencia consumida o disipada por cada uno de los componentes.

Para encontrar la potencia total (P_T​) del circuito serie, simplemente sumamos las potencias disipadas por cada resistencia individual:

Este cálculo nos da una medida del consumo energético global del circuito.

Para verificar si el cálculo individual de potencias es correcto, podemos calcular la potencia total de una segunda manera, utilizando los valores totales del circuito equivalente (tensión total y corriente total).

Esta verificación debe coincidir con la suma de las potencias individuales.

Alternativamente, si se desea calcular la potencia total directamente a partir de la R_T:​

Ejemplo: Potencias de cada resistencia y potencia total

Continuando con el ejemplo anterior, si V_T = 12 V, R_T = 60 Ω, e I_T = 0,2 A, cuyas caídas de tensión en las resistencias eran V₁ = 2 V, V₂ = 4 V y V₃ = 6 V. Calcular las potencias de cada resistencia y la potencia total, verificando con el circuito equivalente.

– Potencias individuales:

– Suma de potencias:

– Verificación con el circuito equivalente:

El Divisor de Tensión

El divisor de tensión es, quizás, la aplicación más importante del circuito de resistencias en serie. Aprovecha el principio de que el voltaje se reparte a través de las resistencias de un circuito serie en proporción a sus valores óhmicos.

Introducción al Divisor de Tensión

A menudo, en electrónica, disponemos de una fuente de alimentación principal (por ejemplo, 12 V o 5 V) pero necesitamos un voltaje menor y muy específico (por ejemplo, 3,3 V o 1,8 V) para alimentar un componente o para que un microcontrolador pueda medir una señal.

El divisor de tensión es un circuito pasivo simple, formado por 2 o más resistencias en serie, que permite escalar o reducir la tensión de la fuente a un valor más bajo y predecible.

La tensión de entrada (V_T) se aplica a los extremos de la cadena de resistencias. La tensión de salida deseada (V_x) se toma a través de solo una de las resistencias (la resistencia de salida, R_x). Dado que la resistencia de salida es solo una parte de la resistencia total (R_T), la tensión de salida será solo una fracción de la tensión de entrada.

Fórmula del Divisor de Tensión

Aunque ya hemos calculado las caídas de tensión individualmente usando la Ley de Ohm (V_x = I_T · R_x), la fórmula del divisor de tensión nos permite saltar el paso de calcular la corriente total, haciendo el cálculo mucho más rápido.

La tensión a través de cualquier resistencia R_x es directamente proporcional a su relación con la resistencia total del circuito (R_T).

La fórmula general del divisor de tensión es:

donde:

V_x es la tensión de salida (la caída de tensión) a través de la resistencia R_x.

V_T es la tensión total aplicada a toda la cadena en serie.

R_x es el valor de la resistencia específica donde se mide la tensión de salida.

R_T es la resistencia total de la cadena en serie (R₁ + R₂ + …).

El término (R_x / R_T) se conoce como el factor de división y siempre será un número entre 0 y 1. Este factor nos dice qué fracción del voltaje total aparece a través de la resistencia R_x​.

Si aplicamos la Ley de Ohm al circuito equivalente de resistencias en serie:

Y por último, se aplica la Ley de Ohm a la resistencia R_x para obtener la tensión V_x:

Divisor de Tensión en los Sensores Resistivos

El divisor de tensión no solo se usa para obtener voltajes fijos, sino que es la base para interactuar con el mundo físico a través de sensores resistivos.

Un sensor resistivo es un componente cuya resistencia (Rx) cambia en respuesta a una variable física externa (luz, temperatura, fuerza, etc.). Al colocar este sensor en un divisor de tensión, convertimos variación de resistencia en variación de voltaje, una señal que los microcontroladores (como Arduino o Raspberry Pi) pueden leer fácilmente.

Como ejemplos comunes tenemos:

● Sensores de temperatura (termistores NTC): su resistencia disminuye (coeficiente de temperatura negativo) cuando aumenta la temperatura.

El termistor NTC se inserta en un divisor de tensión. Para ello, se coloca el NTC en serie con una resistencia R_x. Cuando la temperatura aumenta, R_NTC disminuye, respecto a R_x. El efecto es que R_x aumenta respecto a R_NTC, traduciéndose en un aumento de la tensión de salida V_x.

Se observa en la fórmula del divisor, que si aumenta R_x también se incrementa V_x, proporcionando una señal de voltaje que refleja el nivel de temperatura.

● Sensores de Luz (LDRs - Fotorresistencias): su resistencia disminuye drásticamente a medida que aumenta la intensidad de la luz.

De forma similar al termistor, el LDR se usa en un divisor de tensión. El sensor LDR se coloca en serie con una resistencia R_x. Un aumento de la luz causa una disminución de R_LDR que se traduce en un aumento relativo de R_x. El incremento de V_x permite al circuito medir digitalmente la luz ambiental.

En resumen, el divisor de tensión es un puente entre una fuente de alimentación fija y las necesidades variables y dinámicas tanto de la alimentación de componentes como de la adquisición de datos de sensores.

Ventajas y Desventajas de las Resistencias en Serie

La conexión en serie, a pesar de su simplicidad, presenta un conjunto claro de beneficios y limitaciones que son importantes para el diseño y la solución de problemas en cualquier sistema eléctrico o electrónico.

Ventajas de la Configuración en Serie

Las ventajas de esta conexión se derivan directamente de sus principios fundamentales, haciendo que sea la opción ideal para aplicaciones específicas de control.

● Simplicidad de diseño y montaje: es la configuración de cableado más intuitiva. Los componentes se conectan de extremo a extremo, lo que minimiza la complejidad en el diseño del circuito impreso (PCB) o en el montaje físico. Los cálculos son sencillos (principalmente sumas para la resistencia total), lo que facilita el análisis manual y la rápida resolución de problemas.

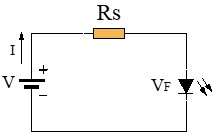
● Control uniforme de corriente: tener el control sobre la corriente es indispensable para proteger componentes sensibles. Por ejemplo, los LEDs (diodos emisores de luz) requieren una corriente muy específica. Conectar una resistencia en serie Rs (llamada resistencia limitadora de corriente) es el método más simple y efectivo para asegurar que la corriente total del circuito no exceda el límite seguro del LED, evitando que se queme.

● Generación de voltajes múltiples (divisor de tensión): la principal fortaleza de la conexión en serie es la capacidad de repartir la tensión de la fuente. El uso como divisor de tensión permite tomar una única fuente de alimentación y generar varios niveles de voltaje más bajos y estables simultáneamente, simplemente midiendo la caída de tensión a través de diferentes puntos de la cadena. Esto es fundamental para sensores y para alimentar circuitos lógicos de bajo voltaje.

Desventajas de la Configuración en Serie

Las limitaciones de los circuitos serie a menudo surgen de su característica definitoria: el camino único.

● Punto de fallo único (efecto "circuito abierto"): es la mayor desventaja. Si una sola resistencia falla (se abre), se interrumpe todo el circuito. Es como las luces navideñas antiguas: si se fundía una bombilla, todas se apagaban. Como consecuencia, la confiabilidad del circuito completo es igual a la confiabilidad de su eslabón más débil. Un solo componente defectuoso paraliza todo el sistema.

● División de voltaje (inflexibilidad): el voltaje de la fuente se divide entre las resistencias. El voltaje en cada una depende de su valor óhmico. La consecuencia es que no se puede obtener un voltaje específico en un punto del circuito sin afectar a todos los demás. Si se necesita un voltaje constante para un componente en particular, la configuración en serie es muy inflexible.

● Imposibilidad de control independiente: no es posible encender, apagar o controlar individualmente cada resistencia o dispositivo conectado en serie. Por ejemplo, no se puede apagar una lámpara en un circuito de lámparas en serie sin apagar las demás. Todas están "atadas" entre sí.

● Resistencia total siempre aumenta: a diferencia del paralelo, donde la resistencia equivalente disminuye, en serie la resistencia total siempre es mayor que la resistencia individual más grande. Esto puede ser indeseable si se busca una resistencia total baja para permitir mayor corriente.

También te puede interesar:

Carga Eléctrica

Voltaje

Corriente Eléctrica

Resistencia Eléctrica

Ley de Ohm

Potencia Eléctrica

Energía Eléctrica

Resistencias en Paralelo

Circuito Mixto

Multímetro

Pinza Amperimétrica