
Gráficos de Iluminación: Curvas Fotométricas, Diagrama Polar e Isolux
Cada luminaria tiene una 'huella dactilar' única: la forma en que reparte la luz. Como la luz no se emite igual en todas direcciones, utilizamos los gráficos de iluminación.
El Sólido Fotométrico representa el volumen de luz en 3D, pero para trabajar en planos usamos su 'corte' en 2D: el Diagrama Polar (o curva fotométrica), fundamental para interiores, y las Curvas Isolux, que funcionan como un mapa topográfico de luz, esenciales para diseñar el alumbrado de calles y carreteras.
La teoría de la luz, con sus magnitudes y leyes, es esencial para cálculos básicos de iluminación, pero simplifica la realidad al usar modelos ideales, como fuentes puntuales que emiten un flujo luminoso de manera uniforme en todas las direcciones.
En la práctica, la distribución espacial del flujo luminoso emitido por una luminaria varía significativamente. Los gráficos y diagramas de iluminación nos permiten visualizar y analizar de manera precisa cómo se distribuye la luz en el espacio. De este modo, podemos seleccionar las luminarias más adecuadas para cada aplicación.
En cualquier cálculo de iluminación la correcta elección y distribución de las luminarias es fundamental para garantizar un nivel de iluminación adecuado.
Un diseño de iluminación deficiente puede dar lugar a problemas como deslumbramientos, sombras excesivas o una distribución de luz no uniforme, pudiendo afectar tanto a la eficiencia energética como al confort visual de los usuarios.
Contenidos
El Diagrama Polar: Cómo leer la Distribución Luminosa
Los diagramas polares o curvas de distribución luminosa son herramientas gráficas que representan la intensidad luminosa de una fuente de luz en función de la dirección de emisión, proporcionando información sobre cómo se distribuye la luz emitida en diferentes planos y ángulos.
En los diagramas polares la intensidad luminosa I se representa mediante un sistema de 3 coordenadas (I, C, γ).
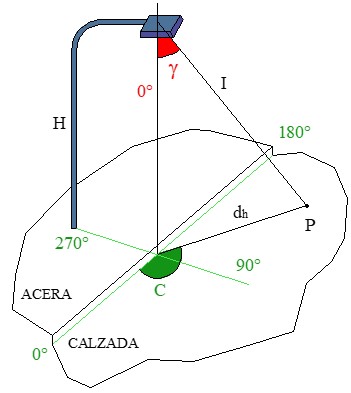
● Coordenada I: esta coordenada indica el valor numérico de la intensidad luminosa I en candelas (cd). En el gráfico, este valor se asocia con la longitud de un vector, que indica cuánta luz emite la luminaria en una dirección específica.
● Coordenada C: esta coordenada define el ángulo del plano vertical en el que se mide la intensidad luminosa. Este ángulo es fundamental para situar la dirección de la luz en relación con la posición de la luminaria:
– Entre 0º y 180º: representan la luz emitida hacia el lado de la calzada o el área a iluminar.
– Entre 180º y 360º: corresponden a la luz proyectada hacia la acera o el entorno opuesto al área principal de iluminación.
– 90º y 270º: son perpendiculares al bordillo correspondiendo respectivamente a la calzada y a la acera.
● Coordenada γ: esta coordenada mide el ángulo de inclinación de la intensidad luminosa respecto al eje vertical de la luminaria. Describe cómo se distribuye la luz en relación con su ángulo de emisión:
– 0º: indica la dirección hacia abajo (vertical).
– 90º: marca la dirección horizontal.
– 180º: representa la dirección hacia arriba, es decir, cuando la luz se proyecta en la vertical inversa.
Al combinar estos tres parámetros, es posible determinar cómo se comporta la luminaria en términos de la distribución de luz, tanto en planos verticales como horizontales.
El Sólido Fotométrico (La Luz en 3D)
Si consideramos todos los vectores posibles de la intensidad luminosa I en todas las direcciones del espacio, obtenemos lo que se denomina un sólido fotométrico. Este sólido es una representación tridimensional del comportamiento lumínico de una fuente de luz.
Sin embargo, trabajar en 3 dimensiones es complejo, por lo que este sólido fotométrico se simplifica utilizando cortes en planos verticales.
Cada corte del sólido fotométrico en un plano vertical genera una curva de distribución luminosa para un ángulo C específico.
Las luminarias que presentan simetría (por ejemplo, las lámparas con distribución homogénea) requieren menos planos verticales para describir completamente su comportamiento lumínico. Sin embargo, las luminarias asimétricas o de diseño complejo requieren más planos verticales para obtener una descripción precisa.
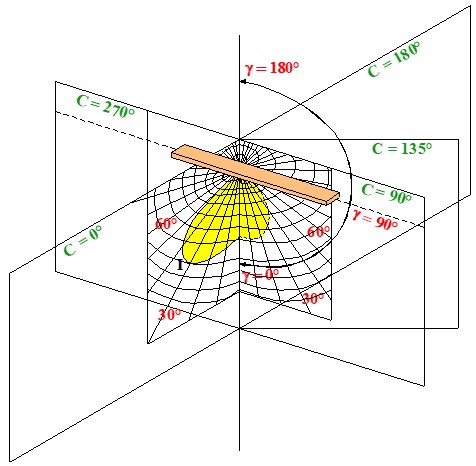
Curvas Polares
En la práctica, los diagramas polares suelen representarse en 2 dimensiones, donde:
– Los radios del gráfico polar representan el ángulo γ, es decir, la inclinación respecto al eje vertical de la luminaria.
– Las circunferencias concéntricas en cada plano vertical indican el valor de la intensidad luminosa I en candelas.
La curva de distribución luminosa del sólido fotométrico corta con los planos verticales considerados de ángulo C específico.
Al analizar un sistema de iluminación, se suelen considerar principalmente 2 planos verticales definidos por el ángulo C: el plano longitudinal C = 0° y el plano transversal C = 90°. En ocasiones se representa el plano en el que la lámpara emite su luz con mayor intensidad luminosa I.
Tal como se observa en la siguiente figura de la curva polar o de distribución luminosa, los radios representan el ángulo γ, y las circunferencias concéntricas el valor de la intensidad luminosa I, en candelas.
Para facilitar la comparación entre diferentes luminarias y evitar tener que generar un gráfico para cada potencia o flujo luminoso, las curvas de distribución luminosa se normalizan.
Esta normalización se realiza respecto a un flujo luminoso de 1.000 lúmenes (lm), permitiendo analizar el comportamiento de la luminaria con una potencia de referencia.
Si se desea conocer el valor real de la intensidad luminosa para una luminaria específica, se debe utilizar la siguiente fórmula:
donde:
Ireal = intensidad luminosa real de la luminaria.
Φ = flujo luminoso real de la lámpara (en lúmenes).
Icurva = valor de la intensidad luminosa obtenido de la curva para flujo de 1.000 lm.
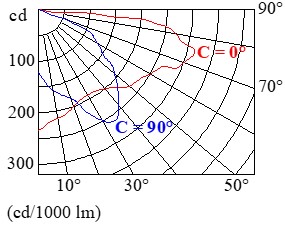
Ejemplo: Si tuviéramos una farola de flujo luminoso Φ = 10.000 lm con el diagrama polar anterior, y si considerásemos una dirección de C = 90º (plano vertical de la calzada perpendicular al bordillo) y γ = 30º (inclinación respecto al eje vertical de la luminaria), ¿Cuál sería la intensidad luminosa en esa dirección?
Obtenemos de la gráfica, para C = 90º y γ = 30º, que Icurva = 250 cd. Entonces:
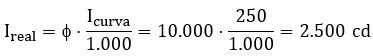
Ejercicios Resueltos de Diagramas Polares
A continuación, se presentan 3 ejercicios resueltos de los diagramas polares o curvas de distribución luminosa que representan la intensidad luminosa I.

Ejercicio 1: Gráficos y diagramas de iluminación

Ejercicio 2: Gráficos y diagramas de iluminación

Ejercicio 3: Gráficos y diagramas de iluminación
Curvas Isolux: El "Mapa Topográfico" de la Luz
Las curvas isolux son herramientas gráficas que permiten representar la distribución de la iluminancia E en una superficie. La iluminancia es una medida de la cantidad de luz que incide sobre una superficie y se expresa en lux, donde 1 lux equivale a 1 lm/m².
El diagrama isolux conecta puntos que reciben la misma cantidad de luz, proporcionando una visión clara de cómo se distribuye la iluminación en una superficie determinada.
Estas curvas son especialmente útiles en el diseño de alumbrado exterior, como en el caso de alumbrado público, donde permiten visualizar de manera rápida cómo las luminarias afectan a la distribución de la luz en las calles.
Como su nombre indica, las curvas isolux representan líneas en las que todos los puntos tienen la misma iluminancia E. En otras palabras, son contornos en un plano que conectan todos los puntos donde el valor de la iluminancia es igual.
Representación y Uso de las Curvas Isolux en Alumbrado Público
En el ámbito del alumbrado público, las curvas isolux son extremadamente útiles para evaluar la efectividad de las luminarias en términos de cómo iluminan la calzada, las aceras y otras áreas adyacentes.
Estas curvas permiten visualizar de un solo vistazo la uniformidad de la iluminación, identificar posibles zonas de sombra o áreas mal iluminadas y optimizar la ubicación y el tipo de luminarias que se van a utilizar.
Lo habitual es representar las curvas isolux en valores absolutos para una referencia estándar de:
– Flujo luminoso: de 1.000 lúmenes (lm).
– Altura de montaje: de 1 metro (m).
Al utilizar estos valores de referencia, es más sencillo realizar comparaciones y extrapolar los resultados a otras configuraciones de altura H o flujo luminoso Φ, que son variables en el diseño de proyectos de iluminación. De esta forma, el cálculo se normaliza y se ajusta más fácilmente a diferentes condiciones prácticas.
Coordenadas Relativas y Relaciones Geométricas
Un aspecto fundamental en la interpretación de las curvas isolux es la relación dH/H, es decir, entre la distancia horizontal dH al punto de interés en la superficie y la altura H de la luminaria.
Esto es importante porque la distribución de la luz y la iluminancia en un punto no dependen solo de la intensidad I de la fuente de luz, sino también de la geometría de la instalación.
Por ejemplo, dH/H = 1,5H indica que el punto de interés está a una distancia horizontal igual a 1,5 veces la altura de la luminaria.
Como se observa en la gráfica, hay 2 distancias horizontales dH, la longitudinal paralela al bordillo de la acera (eje horizontal) y la transversal perpendicular al bordillo (eje vertical).
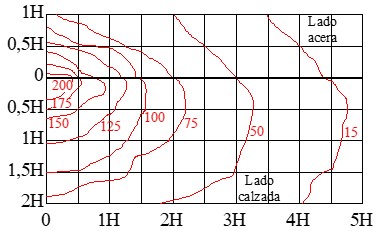
Conociendo la altura H de una farola y la distancia horizontal dH del punto a ésta, la coordenada sería la dH/H. Esto simplifica los cálculos, ya que solo se necesita conocer la relación dH/H para determinar la iluminancia en un punto específico utilizando un diagrama de luminaria, en este caso, el diagrama isolux.
Ejemplo: Tenemos una farola con una altura de montaje de H = 1 m y un flujo luminoso de 1.000 lúmenes (lm). Queremos determinar la iluminancia en un punto ubicado en la calzada, a una distancia horizontal de dH = 0,5 metros de la vertical de la farola.
Estaríamos en la coordenada perpendicular al bordillo (en el lado de la calzada) de:
Esto significa que el punto de interés está a una distancia equivalente a la mitad de la altura de la farola.
Observamos en el gráfico de curvas isolux, que para una luminaria de referencia de 1.000 lm y H = 1 m, la iluminancia E en el punto perpendicular al bordillo de coordenada 0,5H es de 175 lux.
Cálculo de la Iluminancia Real en Diferentes Condiciones
En la práctica, las luminarias estarán montadas a alturas diferentes a 1 metro y podrán emitir cualquier flujo luminoso diferente a 1.000 lúmenes. Para calcular la iluminancia real en esos casos, es necesario ajustar los valores obtenidos de las curvas isolux utilizando la siguiente fórmula:
donde:
Ereal = iluminancia real en el punto considerado.
Ecurva = iluminancia obtenida de las curvas isolux para 1.000 lm y 1 m de altura.
Φ = flujo luminoso real de la lámpara.
H = altura real de la luminaria.
Este enfoque permite escalar las curvas isolux estándar a cualquier configuración de luminaria y altura.
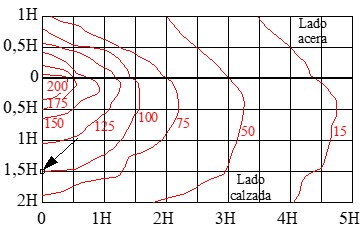
Ejemplo: Supongamos que la farola tiene una altura de H = 4 m con flujo luminoso de Φ = 10.000 lm. Calcular la iluminación E aproximada que habría en un punto situado en la calzada a una distancia del eje transversal de la farola dH = 6 m.
La coordenada que corresponde sería:
Según las curvas isolux, esta coordenada 1,5 H perpendicular al bordillo, en el lado de la calzada, corresponde a Ecurva = 100 lux.
Entonces, la iluminación real Ereal sería:
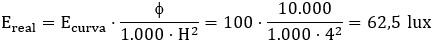
Ejercicios Resueltos de Curvas Isolux
A continuación, se presentan 2 ejercicios resueltos de las curvas isolux que representan líneas en las que todos los puntos tienen la misma iluminancia E.
También te puede interesar:
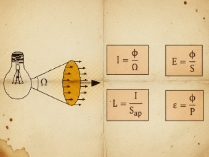
Magnitudes Luminotécnicas: Flujo, Intensidad, Iluminancia y Luminancia
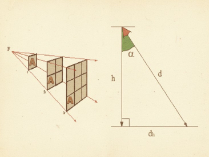
Leyes Fundamentales de la Luminotecnia: Inversa del Cuadrado y Coseno de Lambert

Tipos de Lámparas y Bombillas: Clasificación y Características (LED, VSAP, Halógenas)

Tipos de Luminarias: Clasificación Interior, Exterior y Técnica

Cálculo de Alumbrado Interior: Método de los Lúmenes Paso a Paso

Cálculo de Alumbrado Exterior y Público: Diseño Vial y Normativa



