Leyes Fundamentales de la Luminotecnia: Inversa del Cuadrado y Coseno de Lambert
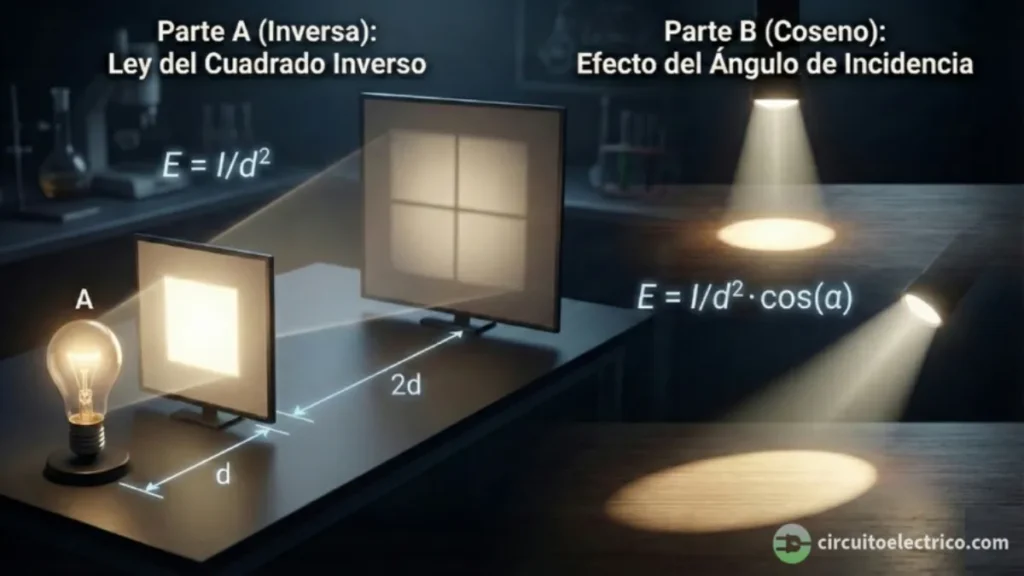
Las leyes luminotécnicas son los principios físicos que explican por qué una linterna alumbra menos cuanto más nos alejamos de la pared. Se basan en dos pilares: la Ley de la Inversa del Cuadrado (la luz se 'diluye' con la distancia) y la Ley del Coseno de Lambert (la luz es menos efectiva si golpea la superficie con inclinación). Combinando ambas, podemos calcular la iluminancia E exacta en cualquier punto debajo de un foco.
Los software de diseño de iluminación utilizan algoritmos basados en las leyes luminotécnicas para simular la distribución de la luz en un espacio. Estos programas permiten visualizar y evaluar diferentes configuraciones de luminarias antes de su instalación.
La ley del inverso del cuadrado de la distancia establece que la iluminancia E sobre una superficie es inversamente proporcional al cuadrado de la distancia d que separa la superficie de la fuente luminosa.
La ley del coseno establece que la iluminancia E sobre una superficie es directamente proporcional al coseno del ángulo de incidencia α de los rayos luminosos sobre dicha superficie.
El cálculo de la iluminación requiere combinar estas leyes con otros factores, como el tipo de luminaria, la distribución de la luz, el nivel de iluminancia y la uniformidad de la iluminación, pudiendo así crear ambientes visuales confortables y funcionales.
Contenidos
Ley de la Inversa del Cuadrado (E = I / d2)
Una de las leyes fundamentales en la luminotecnia y de mayor aplicación en fotografía es la ley del inverso del cuadrado de la distancia.
Esta ley de la iluminación establece una relación matemática entre la intensidad de la luz que incide sobre una superficie y la distancia que separa esa superficie de la fuente luminosa.
La ley del inverso del cuadrado de la distancia postula que la iluminancia E, es directamente proporcional a la intensidad luminosa I de la fuente y es inversamente proporcional al cuadrado de la distancia d que separa la fuente de la superficie.
Se supone que el foco de luz está suficientemente alejado de la superficie (luz procedente de un punto) y que la superficie es perpendicular a la dirección del rayo de luz. Matemáticamente, se expresa como:
Así, si deseamos incrementar significativamente la iluminación sobre un objeto, una estrategia efectiva consiste en disminuir la distancia entre el objeto y la fuente de luz.
Concretamente, reduciendo a la mitad esta distancia, conseguiremos que el objeto reciba cuatro veces más luz.
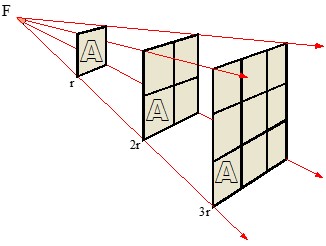
Además de la intensidad luminosa I y la distancia d, otros factores pueden influir en la iluminancia E de una superficie:
– Ángulo de incidencia: la iluminancia también depende del ángulo de incidencia de los rayos luminosos sobre la superficie.
– Absorción y reflexión: los materiales de los que están hechos los objetos absorben o reflejan la luz en diferentes proporciones.
– Dispersión de la luz: la atmósfera, el polvo y otros elementos pueden dispersar la luz, reduciendo la iluminancia.
Se observa que ley del inverso del cuadrado de la distancia relaciona los conceptos de intensidad luminosa I y de iluminancia E.
La demostración de esta ley es sencilla. Según las definiciones de E y de I:
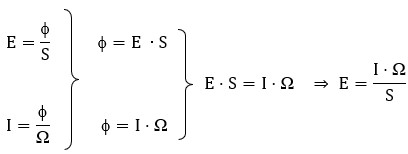
Teniendo en cuenta que el ángulo sólido Ω es:
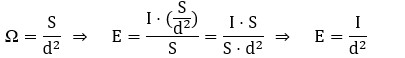
Ley del Coseno de Lambert (El Ángulo de Incidencia)
Si la Ley de la Inversa del Cuadrado nos decía que la luz se debilita con la distancia, la Ley de Lambert nos explica por qué la luz "se estira" y pierde fuerza cuando no golpea una superficie de frente. Es el concepto que explica por qué el sol calienta menos al atardecer que a mediodía.
Si la superficie no es perpendicular a la dirección de los rayos luminosos, la superficie S iluminada es mayor, pero la iluminación E es menor.
Este factor (cos α), que depende del ángulo de incidencia α, disminuye a medida que el ángulo aumenta, reduciendo así la cantidad de luz que incide por unidad de área.
Debemos diferenciar entre estos 2 conceptos:
● Superficie aparente Sap: proyección de la superficie real sobre un plano perpendicular a la dirección de los rayos de luz.
● Superficie iluminada S: superficie total que recibe la luz, independientemente del ángulo de incidencia. En la siguiente figura se observa que el ángulo que forma la superficie aparente Sap con la superficie iluminada S es precisamente el ángulo de incidencia α.
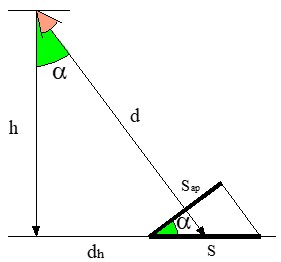
De forma que será:
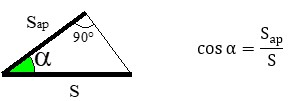
Cuanto más alejada esté la superficie del foco mayor será el ángulo α y menor el cos α. La superficie iluminada S será mayor:
En cambio, la iluminación E se reducirá según el mismo factor (cos α). Por ello, la iluminancia E será:
Podemos enunciar que: “La iluminación E es directamente proporcional al coseno del ángulo de incidencia”.
La Fórmula Combinada (Punto a Punto)
Cuando un ingeniero proyecta la iluminación de una calle o una nave industrial, no solo le interesa saber cuánta luz hay justo debajo de la lámpara, sino cuánta llega a los puntos más alejados. Para ello se utiliza la fórmula combinada de la iluminancia horizontal, conocida como el método de "punto a punto".
Esta fórmula es la herramienta definitiva porque nos permite calcular los Luxes (lx) en cualquier lugar del suelo conociendo solo la altura h de la farola y el ángulo de la luz o el ángulo de incidencia a. Solo habrá que relacionar matemáticamente h y d.
Aplicando el coseno al triángulo rectángulo formado:
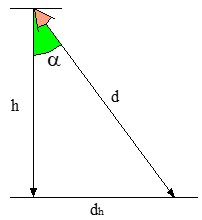
Sustituyendo en la fórmula de la iluminancia E, la ley del coseno de iluminación quedará así:
👉 Resumen de comportamiento:
- A 0º (debajo de la luz): cos3(0) = 1. La iluminación es máxima.
- A 45º: cos3(45) ≈ 0,35. ¡La iluminación ha caído un 65% solo por el ángulo y la distancia!
- A 60º: cos3(60) = 0,125. Solo llega el 12,5% de la luz inicial.
Ejercicios Resueltos de Leyes Luminotécnicas
A continuación, se presentan 5 ejercicios resueltos de cálculo con las leyes luminotécnicas básicas utilizadas en la luminotecnia.
Ejercicio 1: Leyes luminotécnicas
Ejercicio 2: Leyes luminotécnicas
Ejercicio 3: Leyes luminotécnicas
Ejercicio 4: Leyes luminotécnicas
Ejercicio 5: Leyes luminotécnicas
Preguntas Frecuentes sobre las Leyes Luminotécnicas
También te puede interesar:
Magnitudes Luminotécnicas: Flujo, Intensidad, Iluminancia y Luminancia
Tipos de Lámparas y Bombillas: Clasificación y Características (LED, VSAP, Halógenas)
Tipos de Luminarias: Clasificación Interior, Exterior y Técnica
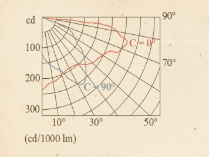
Gráficos de Iluminación: Curvas Fotométricas, Diagrama Polar e Isolux
Cálculo de Alumbrado Interior: Método de los Lúmenes Paso a Paso
Cálculo de Alumbrado Exterior y Público: Diseño Vial y Normativa
